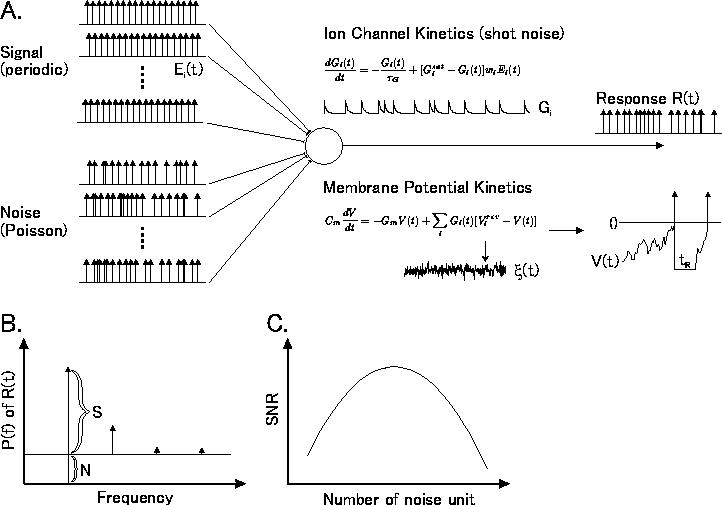
Figure 1: インテグレーター・ニューロンにおける確率共振現象。 文献[6]を模式化。
山本義春：東京大学大学院教育学研究科
平成10年2月28日
横山 コーディネーターの山本先生が演者なので、私、 横山がこの場のコーディネーターを務めさせていただきます。
「生体のゆらぎと神経系のダイナミクス」、東京大学大学院 教育学研究科の山本義春先生です。
山本 横山先生、ありがとうございます。今日は「生体 のゆらぎと神経系のダイナミクス」という題でお話しさせてい ただくわけですが、キーワードとしては、colored noise(有色 雑音)と呼ばれる生体ゆらぎと、近年比較的よく研究されるよう になって参りましたstochastic resonance(確率共振)との関係 ということで、最近の仕事をご紹介いたしたいと思うわけです。 当教室の野崎大地さんとの共同研究でございます。
いきなり本題に入りますと、この ホメオスタシスに関するシンポジウム で第３部をコーディネートさせていただいた意味がなくなりますので、 少し今日これまでの文脈を踏まえて考えてみたいと思います。
神経系のホメオスタシスといったときに、まず一番最初に頭に 浮かぶのは反射という概念であります。これは例えば、感覚 神経によって外界の変化を感知しまして、それを打ち消すように 遠心路に指令を送るということであります。反射調節システムは、 それが紋切り型に動作していればいるほど、自動的な調節能と して優れているということはわかるわけですが、実際にはこの 反射弓にはさまざまなレベルでいわゆる雑音というのが加わり ます。ある場合には感覚器のレベルで物理的な雑音が加わります し、ニューロンを乗りかえる場合には、シナプスのレベル で伝達物質の放出に関してノイズが入ります。あるいはその 結果としてイオンチャンネルが開閉するということ自体も、よく 知られているとおり確率的な現象です。
もう一つは、1つの反射弓を取り上げたときに、午前中、血圧の 調節と関係して最終共通路という概念が出ましたが、そこに 入ってくる信号というのは非常にたくさんあるということです。 例えば1つの反射入力を取り上げたときに別の信号が必ずコヒーレントで ある、関連があるとは限らないということで、こういった多様な 環境の中で神経システムはどういうふうに動くのだろうかという ことが問題になるわけです。
こういうこと自体は、先ほどから話題になっておりますインテ グレーターを使った概念で非常によく研究されております[16] (図1A)。例えばニューロンを1つとりまして、ここに規則的であり、 何らかの情報を持った信号が入って、それが出力に反映される という場合を考えます。ノイズとして、inter-spike intervalが 無相関な、別にこれはPoissonでなくてもいいんですが、そういう ものが入ると想定します。シナプスのレベルでイオンチャンネルが 一過性に開いて、いわゆるshot noiseというものが出て来ます。 これが時空間的に重なり合うと、膜電位のレベルで、shot noiseの 時定数を超えたところでは無相関なwhite noise(白色雑音)みたいな ものが出てきて、これが先ほど合原先生のお話にありましたように 積分されて、閾値に達すると発火するという形で、ある意味では 「計算」がなされるわけです。
Figure 1: インテグレーター・ニューロンにおける確率共振現象。
文献[6]を模式化。
もちろん実際のニューロンでは、このイオンチャンネルはご存じ のように1つではなくて幾つか別のものがありますし、このインテ グレーター自体が、図1Aのように線形システムとして積分されて いるわけでももちろんないわけですが、こういうモデルが考え られるというのは、実は図1Aの出力の統計的な性質が理論的に わかっているというか、計算できるという利点がありまして[16]、 今でもよく用いられています。
さてこのモデルで、図1Aのノイズ・ユニット数を増やして いくと、ニューロンの入出力関係というのは一体どうなるのだろう かというのを調べた人たちがおります[6]。もちろん、 ノイズ・ユニット数を増やしても、信号が規則的にに来て いますので、出力側には信号に対応したパワースペクトルが 基本周波数を中心に観察されるわけですが、同時に無相関の ノイズを加えておりますので、ノイズに対応したパワーも観察され ます(図1B)。このノイズに対して信号はどのくらい大 きいか、いわゆるSN比(SNR)と呼ばれているものですが、 信号入力のユニット数を一定に保っておいて、ノイズのユニット数 をずうっとスキャンしていくと、このSN比があるところで最大になるという ことです(図1C)。そして、SN比が最大になるあたりは、実際には 信号の入っているチャンネル数と同じぐらいの、すなわちノイズが 信号と同じぐらい混ざりあったところであったという結果で、これはある 意味ではちょっと驚きなわけであります。
このことを概念的に説明するのが、いわゆるstochastic resonance
(確率共振)といわれる概念です(図2A)。先ほど図1では、周期的に
インパルスが来ていましたけれども、それが今度は周波数変調
されて、神経細胞の閾値( 
)下で正弦波状にゆらいでいる場合を
考えていただきたいと思うんです。このゆらぎは、入力信号が積分
された結果ということで、入力の情報をある意味で反映している
わけですが、それが閾値に達するまでは全く発火しませんので、
例えば入力に対して出力はどの程度それを反映しているかという
のを見ても、相関は低い、SN比も低い、あるいは入出力の共分散
とか相関係数を計算しても非常に低いレベルにあります。
もう一方の極限では、余り大きなノイズが加わりますと、入力信号と は関係なく発火をしてしまいますので、そうすると入出力の相関は また低くなってしまいます。ある適当なノイズレベルでは、例えば この場合、正弦波の山の部分でうまく発火してくれるようになって、 入出力の間の相関が最高になるわけです。このように、あるノイズ 強度で、神経細胞のような非線形の信号検出システムの検出能が最大 となるという意味で、確率「共振」という言葉が用いられます[5]。 まあ、この辺までが歴史的なハナシということでして、ここで終わって しまっては、全く新しいことがないわけです。
そこで一つだけ、このストーリーにつけ加えることがあるとしますと、
実際にヒトの生理調節システムにみられるゆらぎ、すなわち確率
共振のノイズ項として作用する可能性のあるものには、ほとんどの場合
用いられている白色雑音に加えて、いわゆるcolored noise(有色雑音)と
申しまして、少し変わったタイプのノイズも含まれるということでしょう。
図2B最上段は、コンピュータでつくった白色雑音なのですが、このような
無相関なゆらぎ、あるいは白色雑音を低域通過させた上から2段目のような、
低周波側でスペクトルがフラットになるようなゆらぎというのは、生体
には余りないというか、実はよく調べてみると、対数周波数－対数パワー
軸にパワースペクトルを書いたときに、べきの形でスケールされている
ようなノイズが非常によく見られるということがわかってきたわけです
( 
雑音; 図2B)。べきの形でスケールされるということは、周波数
構造が自己相似性を有するという意味でもありますので、これを
フラクタル的な雑音といったりすることもありますし、低域通過させた
白色雑音に比べて長周期のパワーが非常に大きい、すなわち長期相関を
持つのもその特徴です。
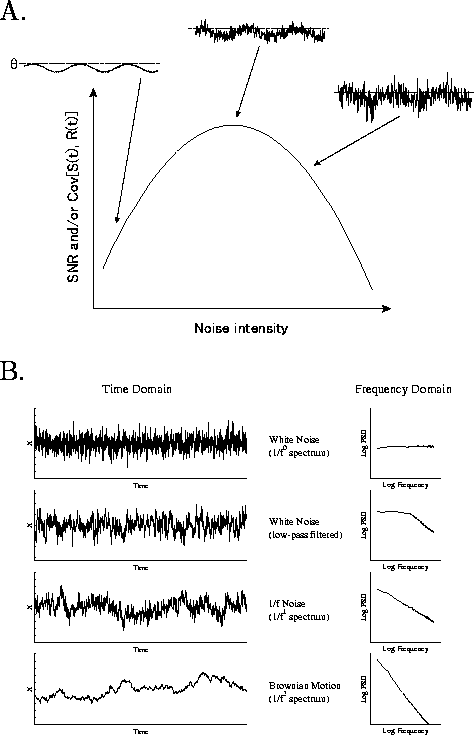
Figure 2: (A) 確率共振の概念図。(B) コンピュータで作成した有色
雑音( ゆらぎ)とそのパワースペクトル。上から2段目は、
白色雑音に低域通過フィルタを施したもの。
これらの有色雑音の例を実際にお見せしたいと思うのですが、まず 感覚神経では、現在はBoston大学におりますLowenとTeichという人 たちが、90年前後、ネコの聴覚神経の発火パターンに有色雑音を見い出して おります[10, 15]。彼らは、聴覚神経の自発発火パターンにみられる 長期相関を評価する目的で、Fano factorと呼ばれる統計量を用いました。 これは例えば、1秒間なり10秒間という観測時間をとりまして、その中に 平均でどのくらいのスパイクが来て(分母)、どのくらいの分散が見られる か(分子)というの計算したものです。よく知られているとおり、もしも スパイクが無相関なPoisson型ですと、平均イコール分散ですので Fano factorは1になります。その意味でPoissonからの乖離度を示す指標 といえましょう。結果として例えばスパイクの観測時間が短いうちは Poissonに近いが、だんだん観測時間を長くしていくと、それに 応じて分散が非常に大きくなって、それがまたべき型にスケールされて いるという興味深い結果が得られました[10]。実際、べき型にスケール されるような系列のinter-spike intervalをスペクトル解析すると、 図2Bのようなべき型のスペクトルを持つことが分かっているからです。
このメカニズムとしては、彼らは、もともとのノイズ自体はランダムに 入るんだけれども、図1Aのようにshot noiseを作る段階で、線形 フィルターと申しますか、通常の1階の微分方程式みたいに自己相関が 指数で落ちるのではなくて、べきで落ちる。こういうものをソースとして また新たなスパイクをつくってやると、実は結果的なスパイクの系列に もべきの関係が残るというようなことを述べています[9]。
次に、午前中も話題になりました心拍動間隔のゆらぎですが、私ども でも特に注目しているのは、やはりこの心拍変動と呼ばれているゆらぎ にも、非常に長周期、長期相関を持つような変動が見られること です[18]。詳細は省きますけれども、この心拍 変動を長時間に渡って計測いたしまして、べき型にスケールされた ノイズの部分をとると、全分散の80～85％ぐらいを占めていて、 スペクトルの傾きがちょうど-1.0というんですから[19]、図2Bの例で いえば、1/f型の雑音ということになります。これは自律神経系の 出力をグロスにあらわしているものだとお考えください。
また、運動神経系についてなんですけれども、これは今Boston大学に行って います野崎さんの仕事です[11, 12]。彼はいわゆる脊髄の 運動ニューロンにおける反射で、単シナプスの反射ということで非常に 扱いやすい伸張反射系を取り上げました。ヒトの筋紡錘からのIa求心性 線維に経皮的に電気刺激を与えまして、単シナプスで、いわゆるＨ反射 というものを誘発するわけです。彼はこれを両脚同時に1 Hz、すなわち 1秒に1回連続的に誘発しまして、そこで得られた筋電図の反射出力の ゆらぎを分析したということであります。
そういたしますと、通常の健常な成人では、左右両脚のゆらぎには非常に 大きな長期相関が見られました。全部で1,050回の刺激を行ったわけ ですから、大体16分くらいの実験なのですが、その16分の間、電気刺激の 強度はもちろん一定なわけです。ところが、出力として見られるゆらぎには 強い長期相関が見られるということがあります[11]。もう一つ 重要なのは、左右両脚のゆらぎのクロススペクトルをとりますと、 低周波側ですごくよく同期しているということがわかりました[12]。 コヒーレンスが低周波のところで非常に高いということです。
一方、同じ実験を脊髄損傷の患者さんで行ってみると、この場合、上位 中枢から脊髄の運動ニューロンにかかっている抑制みたいなものが、 脊髄損傷によってなくなっているという状況なのですが、こういう状況で 同じ測定をすると、反射自体のゆらぎというのが、いわゆる白色雑音に なってしまいます[12]。もう一つは、その時の両脚のゆらぎには、 シンクロが全く見られません[12]。すなわち、いわゆる フラクタル的な雑音が入ってくるとすれば、それはコモンソースというか、 上位中枢に共通の起源を持っている可能性が非常に高いということで あります。
以上をまとめたもが図3であります。まずAは感覚神経であり ますが、先ほど申し上げたネコの聴覚神経の1次求心性線維の発火 パターンには、外界の情報とは恐らく無関係なフラクタル雑音 が入り込んでいます。自律神経系の場合(図3B)、今日午前中も話題に なりましたように出力側が心拍変動ということなのですが、いわゆる 動脈血圧反射システムの入力側には、主には呼吸とか血圧の変動という ものがあるわけです。その上で、呼吸とか血圧の変動には見られない ような1/f雑音というのが入ってきている可能性がどうも高そうだと いうことになります[1, 17, 20]。これについてはまだ異論 もあるんですが。
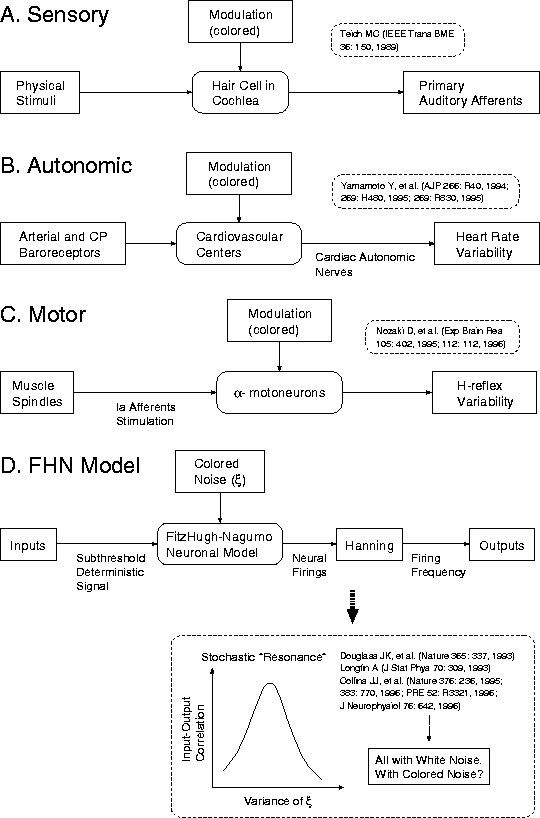
Figure 3: (A)感覚神経、(B)自律神経系、(C)運動神経系における
フラクタルゆらぎ(有色雑音)の起源と、(D)神経モデルにおける確率
共振現象と有色雑音との関係。
もう一つは運動神経系の反射で見ますと、例えば筋紡錘からIa求心性 線維を通して、反射的に筋長を調節しているような伸張反射システムの 場合にも、運動ニューロンのレベルで上位の方から何らかの影響が 加わってきて、それがいわゆる長期相関をつくり出しています(図3C)。
このように私達は、実験で様々な神経調節システムに有色雑音の存在 を確認したり、関連した論文を読んでおりましたところ、そのとき ちょうど、90年代の初頭になりまして、いわゆる生物システムで確率 共振が効いているのではないかというような話になってきたわけです。
そこで用いられた図式というのは大体図3Dのような形式をしておりまし て、入力があって、それを例えば実際の神経なり神経システムが感知 します。感知した後は、インテグレーターでも何でもいいんですが、 神経出力として、発火が起こるとします。情報は瞬時発火頻度に 担われているととりあえず仮定して、出力に例えばHanning窓のような 瞬時発火頻度を求めるようなオペレーションを行い、そして最終出力 を計算します。このシステムにノイズを加えて、例えばノイズの分散なり 強度をスキャンしていくと、入出力間の相関があるノイズ強度で一番 大きくなるという、確率共振の典型的な反応が得られます。そしてこれ が、神経システムにおける確率共振研究の基本的な枠組みということ になります[2, 3]。
ところで、図3をずうっと眺めていますと、何で図3Dに白色雑音を入れて いるんだろう、と思いませんか? 図3A-Cをみる限り、とりあえず ノイズに色をつけてみて、何が起こるのかをやってみたくなるなあという のが人情というもので、最近実際に行ったことはそのようなことだった わけです[13]。
具体的には、図3Dの神経システムとしては、実際のニューロンを使った わけでもありませんし、神経モデルとしてHodgkin-Huxleyモデル[7] でも同じ結果が出ることが最近やっと確認されたんですが、比較的 簡単な方から行こうということで、FitzHugh-Nagumoモデル[4] というものを使いました。
これはv(t)とw(t)という２つの変数を持つ微分方程式の系で
あります。実際のFitzHugh-Nagumoモデルでは、先ほどの閾値 と
いうものが、分岐という現象を通してみられるというように比較的
あいまいな形になっております。すなわち、膜電位v(t)の静止状態と
興奮状態が 4次のポテンシャル関数で仕切られておりまして、これを
超えたときには発火します。そしてw(t)という変数がゆっくりと
静止膜電位側に戻してやる、いわゆるリラクゼーションというダイナミクスを
持っています。先ほどの閾値型(図2A)の場合には、静止・興奮が
クリスプで0, 1になっていて、 を超えると、あとは
コンピュータのシミュレーションをやるときは手で戻してやるわけですが、
この神経は自分で戻ります。後でこのw(t)があることが非常に重要
であるということが出てくるわけですが、上式のようなダイナミクスに
従って、静止－発火を繰り返している神経システムということです。
これに閾値下の信号S(t)を加え、さらにノイズ 
を加えて
やるんですが、このノイズとして、通常の研究で用いられている
白色雑音ではなくて、Gaussian coloredと申しまして、べき型の
スケーリングの係数 
が0から1、そして2へと変わるやつを
入れてやるわけです。結果として観察される神経モデルの発火頻度
というのは、4次のポテンシャル関数の静止側の安定点から、興奮側の
安定点へジャンプする確率R(t)ということになりますが、これは次の
Kramersの公式[8]というもので与えられることがわかって
おります。
このKramersの公式というのは、ノイズ強度Dとポテンシャル・バリア の高さUの関数として、どのくらいの頻度で発火が起こるかということ を記述する公式でして、ここでは信号としてS(t)を入れて おりますので、S(t)の関数としてバリア・ハイトB-S(t)が変化し、 信号に応じた瞬時発火頻度の変化が起こり、それが入出力の相関に つながっているというストーリーで、理論的な扱いができるという意味 でも非常によろしいということになります。
出力として得られたスパイク系列は、これをHanningみたいなウインドーで コンボリューションして、レート・コーディングみたいな形にするわけです。 入出力の相関、すなわち確率共振のパフォーマンスは、次のような指標 で評価します。
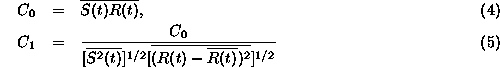
ただし、例えば 
というのは、S(t)を時間平均した
ものです。ここで 
というのは、入力と出力の共分散ですね。
というのは、それを入力、出力の各分散で正規化したものですから、
これは相関係数を表します。
このようなシミュレーションを実際に行ってみると、結果は図4の
ようになります。まずは通常の白色雑音、 
の場合ですが、ノイズの強度が
どんどん上がっていきますと、最初は入出力の相関が高くなって、
しばらくすると落ちていくという典型的な確率共振のパターンが得られ
ます。注目すべきは、私達の体内によく見られるタイプの1/f雑音、
すなわち 
の場合ですが、このとき、他の の値に比べて
圧倒的に小さなノイズで、同じぐらいの共振を引き起こすことができる
ということです。これは長期相関を持っていて --ただ持っているだけ
でしたらブラウン運動( 
)でもいいんですけれども、ブラウン
運動だと、今度はいわゆるリカーシブネス(再帰性)というか、同じところ
にまた戻ってくる頻度が非常に少ないので、そうすると今度は常に
発火を引き起こすわけにはいかない--、かつ適度の再帰性が確保され
ている、ちょうどその境目あたりのところで非常に大きな確率共振現象が
見られるということであります。
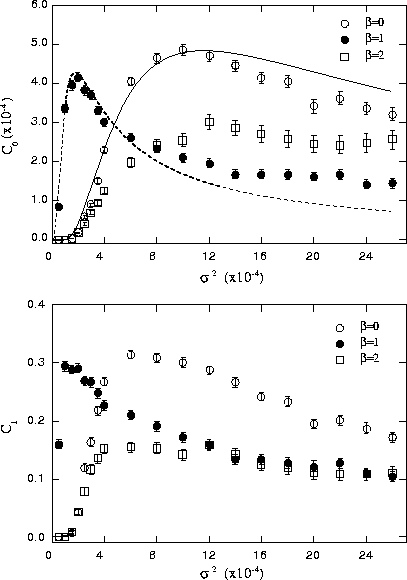
Figure 4: FitzHugh-Nagumoモデルに 型のスペクトルを持つ
有色雑音を印加した場合の入出力間の共分散( )および相関係数( )と
印加した雑音強度( 
)との関係。
私はコーディネーターということで、その本人が遅れてしまっては ちょっと申しわけないので、この辺でまとめに入ります。先ほど リラクゼーションが大事だと申し上げたことは、今回は省きます。 この結果は、今後の研究の指針として、一体どういうことを示唆す るだろうかということ、かなり冒険して考えてみました。
一つは、いわゆる有色雑音、長期相関を持つ雑音というのは、 dynamic complexityと申しますか、動的な複雑性を持つシステムで あれば比較的容易に出すことができるということです。そのような ノイズ様信号がある情報を担っているのだとすると、例えば入力 が2つあった場合、神経細胞のレベルでお互いに高め合うことが できるということです。どちらを信号とみなして、どちらを ノイズとみなすか、という分け隔ては神経細胞にみられる確率共振 現象の場合、最初からあるわけではありませんから。信号が長期相関を 持って、周波数構造がある程度広帯域になると、そういうことが 起こり得るのではないでしょうか。
もう一つは、同じような広帯域のノイズ様成分が2つのニューロンに 入った場合には、例えば最近の例でいうと、FitzHugh-Nagumoモデル にそういった広帯域の信号を入れると、ニューロンの自発発火の 自己相関が非常に高くなって、周期的になってくるという研究が あります[14]。そうすると、このような状況を考えただけで、 ある意味で異なる神経細胞の同期現象のようなものが、ノイズによって 加速されるというようなことも起こりうるのではないかと考えられる わけです。こういうものは、もちろん今は1つとか2つくらいのニューロン で考えているわけですが、それがどんどんつながったときに一体何が 起こるかというのは、ちょっとやってみるとおもしろいかなあという ふうに感じております。
以上をまとめますと、まず生体にはゆらぎがありまして、これは神経系 の紋切り型の反応・反射にはちょっと不都合なのではないかと思われる かもしれませんが、必ずしもそうではない部分があって、それは 確率共振という文脈で扱われてきました。そして、その共振の性能を 高めるのに長期相関を持った1/fゆらぎというのは非常に都合がよい ということです。
二つ目は、これはお時間があれば本当はお話ししたかったのですが、 実はそのメカニズムについても少し仕事が進んでいまして、神経のダ イナミクスが重要であるということです。しかも、ただダイナミックで あるということだけではなくて、いわゆるリラクゼーションの過程が 別にあるということ、神経生理学のことばでいえば相対不応とか、 そういう考え方が非常に重要であるということです。
最後は、先ほど申し上げたように、脳・神経系における情報コーディング を考える上で、ノイズ、あるいはノイズ様の意味のある信号の果たす 役割というのは、少し考えてみたらおもしろいのではないかということです。
以上です。
横山 ありがとうございます。以上の点につきまして、ご質問等が ございましたら……。
栗原 東大の栗原ですけれども、我々やっぱり臨床の立場からいう と、先ほどのニューラルネットの話もそうなんですが、ニューロンの アナロジーとして、それをモデル化して、ニューロンと非常に似た動 態が出るというのをもう一度やっぱり……。先ほどの佐藤先生の質問 とも関連するんですが、実際にニューロンのファンクションをどう説 明するか、何を反映しているのかというのは非常に興味を持つんです けれども。先生の今のFitzHugh-Nagumoのモデルを使われた確 率共振のああいったので、例えば脳でのニューラルトランスミッター による伝達のどういうような側面を反映しているのか。あるいは次の 市丸先生のお話みたいに、ある病的な状態では1/fのゆらぎが 変わってくるというようなことと、何か病的な状態がそこから引き起 こされてくるというような、生理的学的な側面と何かつながりがある かどうかということについて教えていただきたいんですけれども。
山本 恐らく二つあると思うんですが、一つは、例えば FitzHugh-NagumoとかHodgkin-Huxleyを使うのが、実際のニューロン のモデルになるか、あるいはニューラルネットは脳のネットワークの モデルになるかという先ほどからの話題に関してですが、この確率 共振という現象に関しては、実際の神経で同じことが起こるというのが 確かめられていますし、かなりいい実験系が組まれているのも確かなん ですね。そこで用いられたのは白色雑音であります。そして、実際 の神経のモデルとなるシステムで、いわゆる有色雑音が有利に働く という結果が、今日の話のように、例えばわかったとします。わかった というか、それを実際の神経で確かめる前に、仮の実験みたいなものを行っ たわけです。これを受けて、現在野崎さんの共同研究者は、実際の 神経を用いた実験系において、今度は有色雑音を入れみて、本当か どうか確かめようというようなことを計画しているそうです。で すから、そのモデル化自体は、少なくともそういう新しい実験を生み 出すことには役に立つというふうに考えられるのではないでしょうか。
もう一つは、恐らく、有色雑音がなぜ出るかということ、あるい はその長期相関の度合いがどういうふうに病態で変わっていったりとか、 あるいはネットワークの状態で変わっていったりとかすることと関連 していると思うのですが、これはちょっとよくわかりません。という よりも、その起源は、例えば有色雑音に関しては午前中もフラクタルの 話にもありましたように、生体のみでなく物理システム全般にも存在 するわけですから、そもそも共通な起源とかそういうものを求める ことが確かに難しいことなのです。ですから、例えば循環調節なら循環 調節系に、あるいはほかの神経調節系なら神経調節系というように、 個別に探っていかなければいけないということになるかと思うのですが、 そういうような試みは余りよく行われていないということでしょうか。
横山 ほかにございますでしょうか。
久保 女子医大第二病院の久保ですけれども、f分の1のノイズが 入ることで非常に利点というのを先生は強調されたんですが、逆に例 えばお年寄りなんかになりますと、心拍変動なんかでもf自乗に近い ようなノイズが出ますけれども、そういった利点というのは先生方と してはやられてはないんですか。というのは、先ほどノイズがどうい う機序で出るかということに関してはまだいろいろ内部で出る機序は 難しいということでしたけれども、加齢とともにそういうスペクトル が変わってくるということは恐らくそれぞれ利点があって、ただ、あ る方面から見た場合にはf分の1がf自乗に近づくということが不利 に傾いてきて、例えば疾病とかに関連しているのではないかというふ うに私は考えているんですが。
山本 機能的利点という面に関してはおっしゃるとおりですが、 実は、ブラウン運動そのものでFitzHugh-Nagumoをドライブしても、 あまり発火しません。もちろんするところでは沢山発火するんです けれども、しないところでは全くしないので、全体として見ると 入出力の相関はないんです。ただ、ブラウン運動自体は加法過程として 非常に大きな長期相関を持っていますよね。ですから、相関だけが 重要なわけではなくて、ある程度相関を持っていて、そしてある程度、 変な言い方ですけれども、ギザギザしている、その中間ぐらいが 情報のコーディング能を増すという点からはほどよいということだと 思います。そして、そのほどよいノイズが生体に遍在する ということ自体がなぜかという点に関しては、非常に興味深い問題 であろうと思います。例えば加齢でノイズ様成分の相関がブレーク ダウンしていってブラウン運動みたいになっていくと、今みたいな 効果が仮に有効に作用しているとすれば、それは損なわれる可能性が あるわけです。実際例えば、近年問題となっている転倒の問題と 関連して、高齢者の足部感覚とかそういうものを、固有感覚器にノイズを 加えることによって高めてやろうというような応用が始まっている とも聞いております。まだうまくいっているかどうかわからない ですけれども。
横山 よろしいでしょうか。
ありがとうございます。
(「公開シンポジウム 『ホメオスタシスの現在(いま)』. 平成9年度科研費 基盤B・企画調査 『循環系のホメオスタシスとその異常の基本原理に関する 新しい統合的アプローチ』(研究代表者, 大内尉義: 東大医学部老年病科)による, 東京, 1998年2月.」より)
-adrenergic blockade.
Am. J. Physiol., 266(Regulatory Integrative Comp.
Physiol. 35):R40-R49, 1994.
３－４ 生体ゆらぎと神経系のダイナミクス
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 jres_9.
The translation was initiated by Yoshiharu Yamamoto on 1998年06月06日 (土) 14時25分24秒 JST
