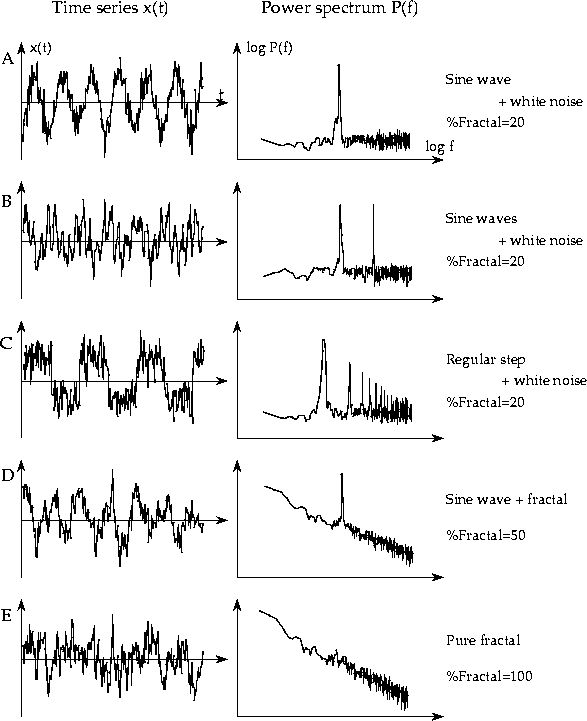
Figure 1: 様々な``非定常''時系列とそのスペクトル 密度。(A)単一正弦波に全分散の20%の白色雑音を加えたもの。(B)複合正弦波に 20%の白色雑音を加えたもの。(C)規則的な矩形波に20%の白色雑音を加えたもの。 (D)単一正弦波に全分散の50%のフラクタルブラウン運動(スペクトル指数
山本義春、大橋恭子 (東京大学大学院教育学研究科)
時系列の定常性という概念は、それぞれの学問分野に応じて細かな 違いがあるものの、平均値、相関関数(あるいはパワースペクトル密度; 以下PSD) などの統計量が測定時刻によらず一定であるという性質を示す。心拍ゆらぎ (心電図R-R間隔の一拍毎の変動)の場合、平均値はもちろん``心拍数'' であり、PSDによって交感・副交感神経系活動が定量 されるのは周知のとおりである。くり返すが、時系列が定常であれば、 平均値やPSDは時刻と無関係にゆらぎに内在する不変的な性質を示す。
少し専門的にいうと、これは得られた時系列を``確率過程''として 捉えた場合のハナシである。例えば図1Aは単一正弦波に全分散の 20%のノイズ(白色雑音)を加えた時系列であるが、確率過程の 理論では、同じ「単一正弦波(+ノイズ)」といっても時刻ゼロで どの位相から始まるかはせいぜい確率的であり、この場合得られた 時系列はいろいろな位相を持つ正弦波のうちの一つがたまたま実現されたと 考える。数学特有の一般化により、考えられる全ての位相を持つ 正弦波について足しあわせれば、平均値はどの時刻でもゼロ、 PSDはお馴染みの線スペクトルである。もちろんこの PSDには時刻を示すパラメーターが含まれていないので定常。 同様のシナリオは、「複合正弦波(+ノイズ)」(図1B)や 「規則的な矩形波(+ノイズ)」(図1C)についても成立する。この場合、 PSDの形の違いが時系列の様相の違いを説明する唯一の要因となっている。

Figure 1: 様々な``非定常''時系列とそのスペクトル
密度。(A)単一正弦波に全分散の20%の白色雑音を加えたもの。(B)複合正弦波に
20%の白色雑音を加えたもの。(C)規則的な矩形波に20%の白色雑音を加えたもの。
(D)単一正弦波に全分散の50%のフラクタルブラウン運動(スペクトル指数
![]() )を加えたもの。(E)純粋なフラクタルブラウン運動(
)を加えたもの。(E)純粋なフラクタルブラウン運動( ![]() )。
スペクトル密度は両対数表示されている。
)。
スペクトル密度は両対数表示されている。
現実には、多くの場合、生体信号は1本の時系列として与えられる。 しかしながら、この時系列が上記のような確率過程からの実現であ るのかどうかということを直接確かめることは難しい(近年話題に なっている``決定論的カオス''の存在は事態をさらに複雑に する -- 詳しくは文献[1]を参照)。そこで次善の策として、 ``考えられる全ての位相を持つ正弦波について足しあわせる''代わり に、ある一定時間の平均的な値をもって様々な統計量を推定する ことになる。心拍ゆらぎの平均値に関していえば、これは例えば1分間の 平均R-R間隔をもって心拍数とするという触診法と同等である。 実は図1A〜1Cの時系列は、平均時間を無限大にした極限で 平均値がゼロになり、PSDも確率過程とみなしたときのもの と一致する(エルゴード的であるなどとも呼ばれる)。そしてこのような 数学的な意味では、これらの時系列は定常である。
ところで、例えば図1Cのような時系列が観察されたとして、これが いわゆる「定常状態」で得られたものと考える生理学者は少ないかも知れない。 もしこれが心拍ゆらぎの時系列であれば、「安静と運動をくり返した ときの心拍数」とか「心拍数の睡眠−覚醒サイクル」などのもっとも らしい解釈を付し、「各々の状態では定常だが全体としては非定常」 と結論づける方が常識的(?)である。ここで「生理学における``定常 状態''と確率過程の``定常性''は別物である」といってしまえば それまでなのであるが、前者の意味での``定常性''を検査する別の 数学的手法を用いれば、図1Aとか1Cの時系列が非定常と判定される 場合もある[2]ことを強調しておく。ただし少し冷めた見方を すれば、これらの時系列が非定常であるといっても、多くの場合その 原因が一目でわかる(あるいは状況からして自明であるということも 考えられる)ものであり、特に「非定常」ということばに秘められた 胡散臭さはない。必要ならば定常とみなせる部分だけ分析するとか、 十分長いデータを用いて統計量を推定するなどの手法を用いれば よいからである。
一方、真の意味で「やっかい」なのは、`` ![]() ゆらぎ''と呼ばれる
図1Dとか図1Eのような時系列である(この名はPSDの対数表示が
対数周波数に反比例することに由来して
いる)。これらの時系列は、スペクトル指数
ゆらぎ''と呼ばれる
図1Dとか図1Eのような時系列である(この名はPSDの対数表示が
対数周波数に反比例することに由来して
いる)。これらの時系列は、スペクトル指数 ![]() が1より
大きい場合確率過程としても非定常であり、上記の生理学的意味に
おいても定常状態とみなされない。加えて、その非定常性に自明な
背景があることも少ないのである。事実、心拍ゆらぎを始めとして様々な
生理学的時系列に
が1より
大きい場合確率過程としても非定常であり、上記の生理学的意味に
おいても定常状態とみなされない。加えて、その非定常性に自明な
背景があることも少ないのである。事実、心拍ゆらぎを始めとして様々な
生理学的時系列に ![]() ゆらぎが観察されているが[2]、その
ほとんどがいわゆる安静時の、一般には定常とされるデータについて
の結果である。心拍ゆらぎにこのような非定常成分が含まれていると
いうことは、平均値(心拍数)のみでなくPSDまでもが
「測定時刻に依存する」ということになり、結果の解釈が極度に困難に
なるであろうことが容易に想像できる。
ゆらぎが観察されているが[2]、その
ほとんどがいわゆる安静時の、一般には定常とされるデータについて
の結果である。心拍ゆらぎにこのような非定常成分が含まれていると
いうことは、平均値(心拍数)のみでなくPSDまでもが
「測定時刻に依存する」ということになり、結果の解釈が極度に困難に
なるであろうことが容易に想像できる。
例えば測定機器のドリフトなどによって時系列にリニアトレンド
(直線的な上昇あるいは下降)が混入した場合、解析を行う前に
明白な非定常要因としてこれを取り除くという方策がとられる。その際、
必ずしもそうとは限らないのであるが、「ドリフトは直線的である」という
``モデル''を用いていることに着目する。同様なことを ![]() ゆらぎに
ついて行えないだろうか。課される条件としては、モデルはできる
限り単純なものの方が望ましい。
ゆらぎに
ついて行えないだろうか。課される条件としては、モデルはできる
限り単純なものの方が望ましい。
非定常性を有する ![]() ゆらぎのモデルのうち最も単純なものの
一つがフラクタルブラウン運動[3]であり(図1E)、
x(n)を離散時系列とすると、
ゆらぎのモデルのうち最も単純なものの
一つがフラクタルブラウン運動[3]であり(図1E)、
x(n)を離散時系列とすると、
という性質を有している( ![]() は集合平均)。パラメーター 0<H<1 は
Hurst指数と呼ばれ、変動の不規則さを変化させる役割を果たす。
(1)式は、時間の尺度をh倍にして構築した時系列x(hn)の
分布型が、大きさが
は集合平均)。パラメーター 0<H<1 は
Hurst指数と呼ばれ、変動の不規則さを変化させる役割を果たす。
(1)式は、時間の尺度をh倍にして構築した時系列x(hn)の
分布型が、大きさが ![]() 倍になる他は、もとの時系列x(n)の分布型と
同一であるという、自己相似(自己アフィン)の性質を示す。それゆえこの
ような性質を持つ変動はフラクタル的であると呼ばれる。もちろん、
フラクタルブラウン運動は
倍になる他は、もとの時系列x(n)の分布型と
同一であるという、自己相似(自己アフィン)の性質を示す。それゆえこの
ような性質を持つ変動はフラクタル的であると呼ばれる。もちろん、
フラクタルブラウン運動は ![]() 型のPSDを持ち、スペクトル指数
型のPSDを持ち、スペクトル指数 ![]() は
は
によって、Hurst指数と結びついている。注目すべきは、一見不規則な
非定常変動が(1)式のような単純な関係式によって表現されており、
Hあるいは ![]() という単一のパラメーターによってこれを表現できる
ということである。
という単一のパラメーターによってこれを表現できる
ということである。
粗視化スペクトル(Coarse Graining Spectral Analysis; CGSA)法[3]は、 このような非定常変動のモデルであるフラクタルブラウン運動と、 図1A〜1Cのような(ある意味では定常な)規則的変動とを分離するための手法で ある。原理的には、変動が純粋なフラクタルブラウン運動で(1)式を 満たすとすると、x(hn) (元の時系列を粗視化したもの) と x(n) は 似通った変動になるが、規則性の強い変動の場合は両者が無関係になるという 性質を利用している。そして与えられた時系列に占めるフラクタル成分の割合 (%Fractal)は前者では100 % となるのに対し(図1E)、ゆらぎに強い周期成分が 混入していたり(図1D)、図1A〜1Cのように規則性の強い変動の場合は、 %Fractal の値も低くなる(CGSA法では白色雑音もフラクタル成分とみなして しまうので図1の例では%Fractal = 0 とはならない)。
このCGSA法を用いてヒトの安静時心拍ゆらぎ8500拍分について解析した
例[4]が図2に示されている。心拍ゆらぎは全体としては ![]() 型の
PSDをもつが、いくつかの周期成分の混入も示唆される(図2B)。これらは
よく知られているように、血圧や呼吸の周期変動によるものである。CGSA 法に
よってフラクタルブラウン運動のみを抽出すると(図2C)、
確かにきれいな
型の
PSDをもつが、いくつかの周期成分の混入も示唆される(図2B)。これらは
よく知られているように、血圧や呼吸の周期変動によるものである。CGSA 法に
よってフラクタルブラウン運動のみを抽出すると(図2C)、
確かにきれいな ![]() 型のPSDが得られる。測定を行なった全20例の平均では、
このようなフラクタル的変動の全分散に占める割合は実に 85.5 % であった。
型のPSDが得られる。測定を行なった全20例の平均では、
このようなフラクタル的変動の全分散に占める割合は実に 85.5 % であった。
![]()
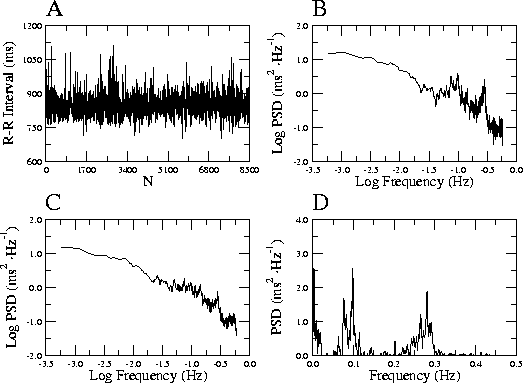
Figure 2: CGSA 法の適用例。ヒト安静時心拍動間隔
(8500 拍分; A)のパワースペクトル(B)と、CGSA 法により抽出したフラクタル
成分のスペクトル(C)。B から C を引くと心拍変動のゆらぎに含まれる周期成分が
現われる。
図1からも明らかなとおり、CGSA法による%Fractal値が高い場合 (図1E、また図1Dでは正弦波を除いた全てがフラクタルブラウン運動なので この場合も該当する)、その時系列には図1A〜1Cにはみられないような 本質的な非定常性があると考えたほうがよい。心拍ゆらぎについても 同様で、このような非定常ゆらぎを残したままで解析を行なったと しても、その平均値やPSDは時間的に``不安定''なものになるであろう。 一方、CGSA法によってフラクタル的変動を取り除いた場合、心拍ゆらぎ の周期成分のPSD(図2D)が時刻に依存しなくなる(定常性をもつ)ことも 示されている[4]。
これまでは、不規則な変動を示す非定常時系列に対してフラクタル ブラウン運動のモデルを設定し解析する方法を述べてきたが、すべての非定常 変動がこのモデルに適合するという保証はない。例えば、乱流のモデルとして 提唱されている間欠性カオスと呼ばれる時系列
は、 ![]() 型のPSDを持ち(従って非定常)、反応性の低い層流相とバーストの
頻発する乱流相が交代的に出現するのが特徴である(図3C)。ただし、その交代が
一見不規則に現われるという点で、図1Aとか1Cの時系列とは異なる。
時間の経過にともなって激しく間欠的に時系列の様相が変化するとの点でフラクタル
ブラウン運動(図3B)とも性質を異にするのだが、CGSA法に
よってこの間欠性カオスの時系列を解析すると%Fractal
型のPSDを持ち(従って非定常)、反応性の低い層流相とバーストの
頻発する乱流相が交代的に出現するのが特徴である(図3C)。ただし、その交代が
一見不規則に現われるという点で、図1Aとか1Cの時系列とは異なる。
時間の経過にともなって激しく間欠的に時系列の様相が変化するとの点でフラクタル
ブラウン運動(図3B)とも性質を異にするのだが、CGSA法に
よってこの間欠性カオスの時系列を解析すると%Fractal ![]() となり、
フラクタルブラウン運動との間に差は認められない。つまりこの場合、
CGSA法の前提となっている「非定常性がフラクタルブラウン運動によって
モデル化できる」という点が満たされないわけで、%Fractal
となり、
フラクタルブラウン運動との間に差は認められない。つまりこの場合、
CGSA法の前提となっている「非定常性がフラクタルブラウン運動によって
モデル化できる」という点が満たされないわけで、%Fractal ![]() と
いう数字にも信頼がおけないのである(もちろん残りの規則的変動が定常であると
いう保証もない)。
と
いう数字にも信頼がおけないのである(もちろん残りの規則的変動が定常であると
いう保証もない)。
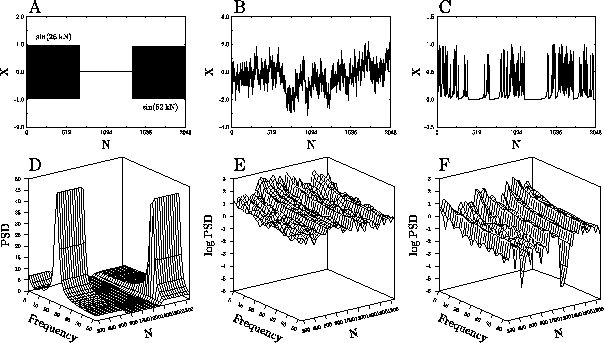
Figure 3: 時系列と Wigner-Ville 分布。
(A)周波数が1/3ずつ変化する正弦波、(B) ![]() の
フラクタルブラウン運動、および (C)
の
フラクタルブラウン運動、および (C) ![]() の間欠性カオス((3)式)に対するWigner-Ville分布が、それぞれ(D)、(E)、
および(F)に示してある。Wigner-Ville 分布の算出は、元信号を
解析信号に変換してから行った。
の間欠性カオス((3)式)に対するWigner-Ville分布が、それぞれ(D)、(E)、
および(F)に示してある。Wigner-Ville 分布の算出は、元信号を
解析信号に変換してから行った。
間欠性カオスの場合、CGSA法で行なったような非定常成分の抽出は 困難であるものの、それでも(3)式のようなモデルが存在する。 しかしながら、一般に全ての非定常変動にモデルが存在するとは 限らず、時間の経過にともなう時系列の統計的性質の変化をありのままに 解析する必要が生ずる。これが時間−周波数解析と呼ばれる解析法である。 時間−周波数解析に用いられる道具としては、スペクトログラム、 ウェーブレット変換、Wigner-Ville分布などがあるが、ここでは通常の スペクトル解析との対応がつきやすいWigner-Ville分布をとり上げる。
今、ある有限エネルギーの実信号をx(t)とし、そのフーリエ変換を X(f)とする。時間−周波数平面上の周辺分布が次の拘束条件
を満たすようなS(f, t)の一つとして、
が挙げられるが、これがWigner-Ville分布である。(6)式から分かるように、 Wigner-Ville分布は時間と周波数の2つの変数をもち、時間に関して積分すると 信号のPSDと一致し((5)式)、周波数に関して積分すると、各時刻での瞬時 パワーが提示される((4)式)。このため、非定常信号の周波数構造が 時間的に変化していく様子を知ることができる。
図3Dは周波数が変化する正弦波の試験信号(図3A)のWigner-Ville分布(ウィンドウ
128点)を算出したものであるが、周波数分解能は決して高いとはいえないものの、
PSDの時間的な変化を比較的よく表現していることが分かる。また、図3Bおよび3Cは、
それぞれフラクタルブラウン運動および間欠性カオスの時系列であり、
それらのWigner-Ville分布を示したのが図3Eおよび3Fである。
フラクタルブラウン運動のWigner-Ville分布は絶対時刻tによらず、
周波数領域では常に
一定の ![]() をもつべき型のPSDを示す(これは数学的にも示される[10])。
それに対して、間欠性カオスのWigner-Ville分布は、特に層流相において
PSDの落ち込みが顕著で、時間の経過にともなう時系列の統計的性質(この場合は
周波数分布)が急激に変化する。
をもつべき型のPSDを示す(これは数学的にも示される[10])。
それに対して、間欠性カオスのWigner-Ville分布は、特に層流相において
PSDの落ち込みが顕著で、時間の経過にともなう時系列の統計的性質(この場合は
周波数分布)が急激に変化する。
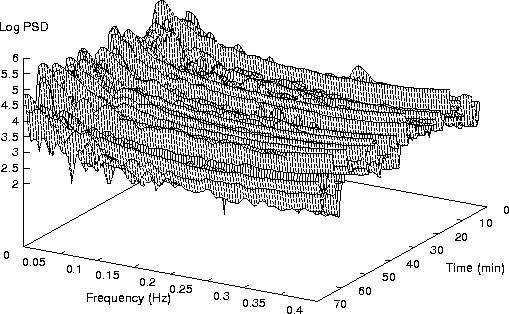
Figure 4: ヒトの安静時心拍ゆらぎのWigner-Ville分布。
約4000拍分について、20拍毎に表示してある。
ヒトの安静時心拍ゆらぎのWigner-Ville分布を同様な方法で解析すると (図4)、フラクタルブラウン運動のように絶対時刻によらぬ比較的安定した PSDが得られる。したがって、ヒトの心拍ゆらぎをフラクタルブラウン運動 としてモデル化し、CGSA法の解析対象とすることにはそれなりの根拠があると いえるだろう。このように、時間−周波数解析は、対象となる非定常性が どのような類のものであるかについての情報を得るためにも用いることが できるのである。
(医学のあゆみ 177: 586 より)
心拍ゆらぎの非定常解析
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 jres_8.
The translation was initiated by Yoshiharu Yamamoto on 1998年06月06日 (土) 14時24分59秒 JST