野崎大地・山本義春 (東京大学大学院・教育学研究科)
数理科学，1997年6月号より
「物理現象の原理」を追求する学問である物理学では， 長い間「ニュートンの法則」が基本原理であった．「生 命現象の原理」を追求する生理学において，それと比肩 しうる基本原理はCannonの「ホメオスタシス」だといえ よう．ホメオスタシス(homeostasis)とは，同一の(homeo) 状態(stasis)を意味するギリシア語からの造語で，「生 体内の組成・物理的状態を一定に維持する機能」を表す 生理学用語として，今世紀初頭のアメリカの生理学者 Walter B. Cannonにより命名された．この原理がいかに 基本的なものかは，生理学のほとんどの教科書の冒頭に ホメオスタシスについての記載がみられることからも理 解できる．これらの記載を要約すれば，「生体が生命 を維持するためには，ホメオスタシスを保つことが必要 である．ホメオスタシスが保たれるのは，生体に負のフ ィードバック回路からなる自動調節機能が存在するから である．」ということになる．
生理学的なパラメータの中でも，生命の維持に直結する 心拍，呼吸，血圧，体温などは，特に総称して生命徴候 （バイタルサイン）と呼ばれる．これらにホメオスタシ スの概念をあてはめると，一定の値（正常値）から外れ るような外乱が加われば，それを補正するようにフィー ドバックがはたらくというのだから，その値が安定して いればいるほど，生体の制御系がうまく働いているとみ なせよう．ところが実際には健常な被検者が安静を保っ ていても，例えば心臓の拍動間隔は一定ではなく，かな り不規則な変動（心拍変動）を示す．呼吸，血圧，体温 なども例外ではない．そして心拍変動に限っていえば， むしろ加齢や病的な状態の方が変動が少ないのである．
物理学において，カオスの概念は，一見意味のなさそう な不規則な挙動が単なる誤差ではなく，非線形性をもつ 決定論的な系（しかも低次元かもしれない）に由来する という可能性を提示してきた．従来は無意味と切り捨て てきたものが，不可避的に現れるというのであれば，逆 にそのゆらぎを積極的に調べていくことで，現象の理解 が深まるのではないかという期待がでてくる．生理学 の分野においても，1980年代半ばから心拍変動や脳波な どの生体信号がカオスではないかという報告が相次いだ． そして最近では生理学の権威あるPhysiological Review誌にカオスのレビューが掲載されるほど [1]，この分野でもカオスを扱った研究が一般的 となりつつある．では，はたして物理学においてカオス理 論に対して抱 かれていた期待が，生理学ではどの程度達成されてきたのだ ろうか？
誌面は限られているが，この小論では生理学におけるカ オスについて現在までの研究の流れを簡単にたどってい きながら，今後の展望についても考えてみたい．
生体の各調節系は非線形であり，カオスが存在すること はあり得ないことではない．たとえばイソアワモチのペ ースメーカーニューロンを周期的に電気刺激するとカオ ス的な応答が生じるというHayashiらの報告 [2]にみられるように，すでに単一ニューロン のレベルにおいてカオスは存在しているのである（単一 ニューロンのレベルにカオスが存在することは，精度の 高い実験からも，数学モデルの振る舞いからもほぼ間違 いないと考えられている）．それでは，このようなカオ ス的な活動がもっとマクロなレベルでも存在し，さらに 生体のなんらかの機能，あるいは活動に関連しているの だろうか？これに答えるためには，まず生体機能が働い た結果として発現す る生体信号がカオス系に由来し ているかどうかを判定する作業が必要となる．
測定されたデータからタケンスの埋め込み定理に従っ てアトラクタを再構成し，相関次元やリヤプノフ指数な どを計算して低次元のカオスか否かを判定するという方 法論は1985年までにほぼ出そろった．それ以降，脳波や 心拍変動などにこうした方法論が適用され，低次元のカ オスを発見したという報告が相次ぐようになった．例え ば，Babloyantzらは，脳波の相関次元が覚醒時に対し， てんかんや睡眠時に比較的低い値になることを報告した [3]．これらの結果によれば，数十億のニューロ ンからなる脳の自発的な活動がたかだか4〜8程度の変数 によって記述できるというのだから，かなりのインパク トがある．しかし，有色雑音や，ある種のフィルタリン グによって相関次元が有限値に収束してしまうという報 告 [4, 5]，カオス判定の統計量の算出に必要な データ数の基準 [6]などから，低次元のカオスの 存在を手放しで受け入れるわけにはいかないようになっ てきた（特に心拍変動をはじめとする生体信号の多くが 有色雑音的な性質をもつ こと [7]が問題を一層複雑にしている）．
現在では，前者の問題への対処法としてサロゲーション の手法が開発され，より慎重にカオスか否かの判定が行 われるようになってきている [8]．サロゲーシ ョンの手法とは，たとえば，あるデータについて得られた相関次元 が，その線形相関に由来するという帰無仮説を， 元データと同じパワースペクトルをもつ確率論的なデー タ（サロゲートデータ：フーリエ成分の位相項をランダ ムにして逆フーリエ変換して得られる）の相関次元との 差異をもって検証するものである．Theilerらはこの手法 を用いて，単極誘導によって得られた脳波を再検討した が（このデータは1989年の段階では相関次元が４程度の カオスとされていたものであった [9]），相関次元の値がサ ロゲートデータと区別がつかないことから，カオスであ るとはいえないと結論している [10]．
サロゲートデータには，主に上記のような（一次の）時 間相関の性質を保存したものを用いることが多いのだが， 生体信号を扱う場合には，違う型のサロゲートデータが 必要となることを指摘しておきたい．生体信号の中には， その分布が正規型ではないものも多い．しかし，こうし た信号の場合でも，時間相関を保存したサロゲートデー タは必ず正規分布となってしまう．分布が全く異なるこ れらのデータを比較することは，土台無理というもので ある．こうした信号に対してはむしろ，「線形な正規 過程から生じた変数が非線形な関数を通して観測され ，一見カオス的な性質をもつに至った．」という 帰無仮説を採用すべきであろう [8]． この帰無仮説を検証するサロゲートデータの作成には， Theilerらの提案した方法 [8]を用いる．その方法とは，まず 正規乱数を元データの振幅の順番に並び替え（要するに 観測前の正規時系列をつくる），それと同じパワースペ クトルをもつデータを作成する．このデータの振幅の並 びに従って，元データを並びかえてやると，振幅の分布 が同じでかつ，観測前の正規時系列の時間相関は同一の サロゲートデータを作成することができる．
現在でも非線形予測をはじめとした時系列の非線形性を
抽出，評価する数々の方法が提案されているように
[11, 12]，時系列解析の方法論は確かに進歩して
いる．一方で，生体のマクロな系から得られるデータは
S/N比が悪い，測定中の定常性が保証できないなど問題も
多く，カオスか否かの判定能力に限界が存在することは認識しておかね
ばならない．そうとはいえ，これらの解析から導出され
る指標それ自体が，臨床において重要性をもつようにな
る可能性を有している．Goldbergerらの有名な主張
[13]は，健常人の心拍変動が不規則なのに対し，
心疾患をもつ患者では規則的になるため，カオス
健康，規則的 不健康とい
うような対応づけができるのではないかということであ
った（ただし，彼らは当初「カオス的」であることと，
不規則であることを同義で用いており，したがってせい
ぜい「不規則 健康」という程度の意味し
かない）．彼らの主張のようにような単純な図式が成り
立つかどうかはわからないが，疾病，加齢によって時系
列の動的性質が変わるということはありそうなことに思
える．このような時系列の動的性質の変化を，非線形時
系列解析から得られる諸指標により定量化し，診断などに
応用するという期待もできる [13, 14, 15]．
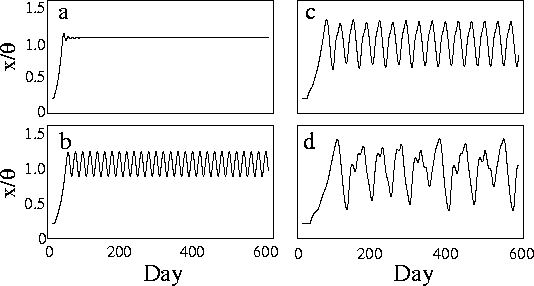
Figure 1: (1)式[17]の解
(n=10, 
, 
)． 
の値は順
に，3 (a) ，6 (b) ，12 (c) ， 20 (d)．
時系列解析によって生体信号がカオス的な性質を有する か否かを同定するというのが，これまでのカオス研究の 主流であった．しかし，カオスらしいと判定されても， そこから逆に調節システムがどのようなダイナミクスを もっているかというようなことを解明することは困難で ある．そこで，それとは逆に，ある経験的事実に立脚し てモデルをつくり，それが予測する挙動と実際の挙動を 比べることによりモデルの正当性を強化するというよう なアプローチが考えられる．
生体のカオス的な挙動に対するモデルによるアプローチ の一例として，MackeyとGlassの研究が挙げられる [17, 16]．生体の調節機構にフィードバックが重 要な役割を演じていることは事実であるが，このフィー ドバックには通常いくらかの時間遅れが伴う．Mackeyと Glassは白血球生成（正確には好中球）のダイナミクスを 次の時間遅れを伴う微分方程式であらわした．
ここで x は白血球の濃度， 
は時間
だけ前の白血球濃度である．式
(1)は，白血球が破壊される割合が
であり，さらに だけ以前の白血球密度
に応じて白血球が生成されることを示す．n や 
は
白血球濃度と生成量の関係を表すパラメー
タである．この微分方程式の定常解は，例えば時間遅れ を
増加させると周期解に分岐し，さらにカオス的
な解に至る（図 1）．実際の白血球濃度は健
常人の場合，ほとんど一定レベルに保たれるか，あるい
は14〜21日周期の弱い振動を示す．ところが，白血病に
冒された患者の場合には振動の振幅が劇的に大きくなる
とともに，不規則な振動パターンを示すようになる．そ
して，患者の多くは細胞の生成に要する時間が長くなっ
ている（すなわち が大きくなる）という．この
MackeyとGlassのモデルは白血球を生成するシステムを
非常におおまかにモデル化したものであるが，それにも
関わらず，病態による白血球濃度の挙動の変化をある程
度説明している．
それにもまして重要なことは，式(1)が， 白血球生成に限らず，生体において普遍的な構造を有し ていることである．式(1)を一般化する と，
となるが（ただし， 
），これは，変量の変
化率が，除去と時間遅れをもった生成とのバランスによ
って決定される系である．ここで関数 f(x) はある時
点の値を元に生成量を決定する非線形なフィードバック
関数である．関数 f(x) としては，大別して，正・負
のフィードバック関数，およびそれらの混合型の３つの
形を仮定できる．ただし，ここでいう正（負）のフィー
ドバック関数とは， 
のとき
（ 
）を満たす
ものであり，混合型とは，ある x に対して f(x)が
最大値をとるような関数のことをいう
．an der Heidenらは，こうしたフィード
バック関数をステップ関数として表した場合について検
討し，正・負のフィードバック関数ではせいぜい周期的
な挙動しか示さないが，混合型のフィードバック関数の
場合にはカオス的な挙動が現れるようになることを解析
的に証明している [18, 19, 20]．
式(2)のようなダイナミクスをもち， かつ関数 f(x)が混合型のフィ ードバック関数（すなわち「こぶ」型である）という系 に類似な系としては，白血球生成系の他にも，いくつか の例を挙げることができる（たとえば代謝調節系，呼吸， 反回抑制神経回路など [19]）．しかし，残念 ながら，これらの系がカオス的な性質を持つ可能性を有 するという推測は，実際のデータとの比較によ って，納得のいくほど確かめられるにはいまだ至ってい ない．麻酔したラットの呼吸パターンのカオス的な挙動 が，フィードバック経路である迷走神経活動に関係している という報告 [21]や，上皮小体ホルモンの分泌がカ オスであるという報告 [22]など，生理学の分野で も時系列解析を基盤としたカオスの存在の可能性を示す データが蓄積されつつある．こうした時系列解析の結果 とモデルによる推論とが相互参照しながらカオスの存在 を探求していくというのが一つの理想であろう．
カオスの概念が生体調節機構について新たな知見をもた らしてくれることが，我々の願いに他ならないのである が，その理想的なシナリオは大まかにいえば，[1]ある生 体信号がカオスであることが証明され，それに基づいて， [2]それを生み出す系のダイナミクスの詳細が解明され る，[3]カオスが生体機能に果たす役割が解明される，と いうことになるだろう．研究が初期の段階では，より本 質的な[2]や[3]を積極的に研究対象としていくには，そ もそも[1]の生体信号がカオスであるのかどうかを確認 する必要があった．その意味で，現在まで主流を占め てきた，時系列解析によってカオスを判定するという研 究は多大な重要性をもつものだったといえよう．
しかし，上記のシナリオは有効にはたらきうるのだろう か．まず注意すべき事に，時系列解析によるカオスの判 定がサロゲーションを用いた帰無仮説の検証という形で 行われる現状では，[1]は100％の確信をもって断言できる ような類のものではない．前節で述べたようなモデルと のアプローチとの相互参照によりカオスの可能性を拡げ ていくことが理想とはいえ，それが実現できるような系 はもともとダイナミクスがある程度分かっているような 単純な系に限られているのが現状である（この場合は， ともすると元のダイナミクスがある程度分かっている のだから，カオスが出るからといって大騒ぎするほどの ことではないのかもしれない）．いずれにせよ，実は[1]， [2]は検証，解明が一筋縄ではいかない困難な問題である こともあり，生理学においてインパクトのある研究結果 はまだ得られていないのが現状である．こうしたある種の行 き詰まりは，生体調節機能においてカオスがどのような 役割を果たしているのかという視点が欠けていたことに 起因しているように思える．[1]，[2]にこだわるの ではなく，むしろ今後，思い切って[3]にも注意を向けることによ って，逆にカオスの存在の正当性などが受け入れられるようになる いうシナリオは考えられないだろうか．
もちろん，明確なものではないが，カオスの存在意義に ついての仮説は提唱されている．例えば，心拍変動につ いて，病態や加齢による時間的な性質の変化についての 考察から，健常者は心臓の拍動間隔を低次元のカオスに 保つことによってより安定した状態を保つことができる のだとするホメオダイナミクスの概念もその一つである [13, 14, 15]．ホメオダイナミクスの概念は， 調節系が，様々な酸素需要の変化 に速やかに追随できることを説明するかもしれない，な どということを我々も空想して喜んだりもするほど興味 ぶかいものである．しかし，カオスの存在の必然性，生 体の機能との関わりについての洞察は現在のところまだ まだ希薄である．
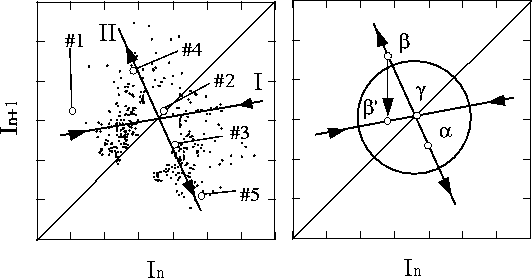
Figure 2: カオス制御の概念図[24]．説明本文．
カオスが生体の調節系に存在するとしても，その存在 意義についてはいまだ我々の理解は十分ではないのだが， その一方で生体に存在するカオスを利用して外部から生 体のリズムを制御しようという試みがなされている．代 表的なカオス制御法であるOGY法 [23]が，in vitroなレベルでウサギの不整脈や [24]，ラット の海馬切片のニューロン群の発火 [25]の制御に 応用され，驚くような成果を得ているのである．
これらの研究で用いられた制御がいかなるものかを
Garfinkelらがおこなったウサギの不整脈の制御を例に
とって説明しよう．横軸にある時点での拍動間隔( 
)，
縦軸にはその次の拍動間隔( 
)をとったもの（ポ
アンカレプロット）を考える（図 2）．規
則的に心臓が鼓動するように制御するためには，このプ
ロット上で直線 
上に軌道を誘導すればよ
い．図上でラベルされたようなプロット列（#1,#2…）
を見つけることができたとする．これらのプロット列は，
Iにそって直線 に近づき（安定多様体），そ
の後IIにそって離れていく（不安定多様体）ことを示し
ている．すなわち，I，IIの交点（不安定平衡点）
は鞍点になっており，周期運動は存在するものの，それが
非常に不安定なことがわかる．
さて，この不安定平衡点はカオスに含まれる周期運動で
あるが，安定多様体を利用して軌道をこの位置に近づけ
るように制御すればよい．そのために，まず図のように
不安定な平衡点の近くに， 
のような軌道が現れ
るのを待つ． は不安定多様体にそって次には
に写されると予想できる．そこで電気刺激を与
え，安定多様体上の 'に写されるようにすると，
あとは安定多様体にそって平衡点に自動的に近づいてい
く．以後は，不安定多様体にそって平衡点から離れていく
場合に適宜，安定多様体の上に落ちるように制御してや
ればよい．Garfinkelらはこの方法により不整脈を規則的
な拍動に制御することに成功した．電気刺激を規則的に
与えてもうまくいきそうなものだが，その場合拍動は規則的に
なるどころかむしろさらに不規則になったという．同様
な方法が，Schiffらにより海馬切片のCA3と呼ばれる部
位のニューロン群の自発的な発火の制御に用いられ成功
を収めた．そこでは，発火間隔を規則的に制御するだけ
でなく，軌道を不安定多様体に導くようにする反カオス
制御が行われ，てんかんの治療への展望が述べられてい
る．
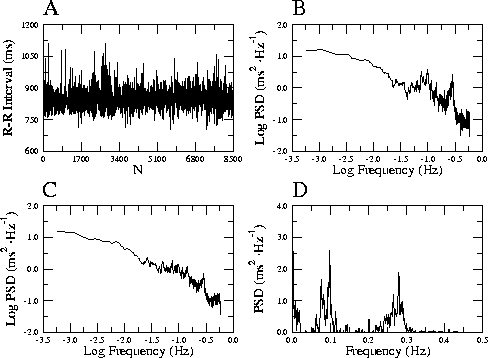
Figure 3: ヒト安静時心拍変動（Ａ）のパワースペクトル
（Ｂ）と，粗視化スペクトル法により抽出したフラクタ
ル成分のスペクトル（Ｃ）．ＢからＣを引くと心拍変動
のゆらぎに含まれる周期成分が現れる（Ｄ）．
カオス制御を生体に応用したこれらの研究は，系にカオ
スが存在する可能性を示し ，さらに臨床面
での可能性を開いたという意味でもちろん重要である．
しかしそれ以上に，カオス的なシステムを持っていれば
それをコントロールすることにより任意の周期状態を実
現することができるという事実は，生体におけるカオス
の役割を考えるうえでも看過できないほど重要な認識を
与えてくれたといえよう．
生体にカオスが存在することの証明は時系列解析に因ら ねばならないが，既述したように100%の確信をもってカ オスであるということは不可能である．にもかかわらず， 生体ゆらぎを決定論的な視点からみていると，問題が決 定論的な系に由来しているかどうかがまず第一義となり， それ以降の発想がその真偽の検証作業に拘束されてしま う危険性がある．我々はこれまで，心拍変動や運動神経 系にみられるゆらぎなどが，１次元のブラウン運動を拡 張したフラクショナルブラウン運動と呼ばれる確率論的 なモデルを用いてうまく記述できることを指摘してきた [7]．そして，このモデルによって抽出された パラメータは，生理調節システムと明確に関連している のである．通常のブラウン運動 B(i) は，白色ノイズ の加法過程として表現され，その分散は
と書けるが（＜＞は集合平均），Mandelbrotはこの性質 を拡張し，
をフラクショナルブラウン運動と呼んだ
[27]．パラメータ 
はハースト
指数と呼ばれ，変動の不規則さを変化させる役割を果た
す．(4)式で 
とおくと，
が導かれる（ただし 
とおいた）．
(5)式は，時間の尺度を h 倍にして
構築した時系列 
の分布型が，大きさが
倍になる他は，もとの時系列 
の分布型
と同一であるという，自己相似（自己アフィン）の性質
を示す．それゆえこのような性質をもつフラクショナル
ブラウン運動はフラクタル的であると呼ばれるのである．
このようなフラクショナルブラウン運動のパワースペク
トルは 
型となり， と H の間に
は 
のとき H=0，
のとき 
なる関
係が成り立つ（ が2のときが通常のブラウン運
動に相当する）．
心拍変動は呼吸や血圧調節に起因する周期的な変動を含
むのだが，それらを粗視化スペクトル法と呼ばれる方法
を用いて周波数領域で取り除いてやると [28]，
健常人の場合，安静時ではほぼ 1/f 型のパワースペク
トルを示す [29]（図 3；通常 1/f ゆ
らぎと呼ばれる）．ところが の値は，循環系の
運動負荷 [30]や重力負荷 [31]によって増
加し2に近づく． が1の場合には
そのフラクショナルブラウン運動は反持続性と呼ばれる
性質（ある過去から現在までに値が増えれば（減れば），
将来には減少（増加）する確率が高い）を持っており，
心拍数をある一定レベルに保つ調節作用がはたらいてい
るものとみなせる． が2に近づくにつれ，通常
のブラウン運動同様に過去から現在
までの増分と現在から将来への増分が独立して生じるよ
うになるので，これを調節能力の減退の結果と捉えるこ
ともできる．実際， の増加は，加齢にともなっ
ても観察される現象である．
このようにフラクタルの概念を用いた場合には，ゆらぎ
の生成メカニズムの解明は第二義的なものとなってしまうが，そのある
がままの動的性質を評価することによって，意味を積極的に考察するこ
とにウエイトが置かれるようになる．そうとは
いえ，フラクタル性の由来についてもある程度のことは
判明している．心拍変動の場合に の値が1とな
るのは，心臓を支配する2種類の神経のうち，交感神経
は無関係で [29]，副交感神経が関係している
[32]ことが薬理遮断による実験より明らかにな
っているし，呼吸や血圧の調節との関連も小さいことが
示されている [33]．こうしたフラクタル性の起源
は脳幹より上位の中枢にあるのだ，といってしまいたいところ
だが，心自律神経系はかなり複雑な構造をもっているた
めそう簡単には結論づけられない．
その点，我々がフラクタル性を発見したヒラメ筋のＨ反
射（図 4）の変動 [34]の場合は，系
が比較的単純ということもあり考察しやすい．Ｈ反射と
は，Ia求心性線維を経皮的に電気刺激することによって
得られる単シナプス反射のことを指す．
高位中枢や様々な末梢器官からの入
力による脊髄αニューロンプールの興奮性の変化を，反射
性の筋収縮に伴って生じる筋電図(EMG)の振幅の大きさに
よって評価できるのである．毎秒1回の電気刺激によっ
て誘発されたＨ反射振幅の時系列から計算した
の値は，健常者の場合には0.9程度になるのに
対し，脊髄上位からの指令が途絶えた脊髄損傷患者では
0.2程度と白色雑音に近いゆらぎの性質をも
つ [35]．この結果は，時系列の 1/f 雑音的
な性質が脊髄上位の構造に由来していることを意味して
いる．
Ｈ反射時系列のフラクタル性が脊髄上位の構造からの調 節の結果だとすれば，その存在の必然性は何であろう か？それにどのような意味があるのかを ，少し冒険をして確率共振の概念を用いた説明 を試みてみたい．確率共振（Stochastic Resonance; SR） とは，神経細胞などの非線形システムへの微弱な入力に 対する応答性が，一定のノイズの存在下で増強されると いう現象を指す [36]．実際，Collinsらは，以下の FitzHugh-Nagumo(FHN)モデル（ i は i 番目のニューロン を示す）
で表されるユニットを N 個並列にならべた系（図
5A）に，閾値下の信号 S(t) が入力した場合の応答を
全ユニットの応答の総和とすると，幅広い雑音レベルで
高い信号検出能が得られることを報告している
[37]．ただし， 
はユニット毎に異なる
ノイズであり， 
とする．
Ｈ反射のフラクタル性の結果，およびCollinsの考えた
系が図 4の伸張反射経路と生理学的に同様な
構造をもつことを考えあわせ
て，我々は高位中枢からの 1/f 雑音様の調節が確率共振に
おけるノイズ源として働くのではないかという仮説をも
つに至った．こうした背景から，Collinsらのモデルにお
いて，白色雑音だけでなく，1/f 雑音やブラウン運動
をノイズ源として用いた場合について検討してみた．
ユニット数 N は100とし，FitzHugh-Nagumo方程式を時間
間隔0.01sで4次のルンゲクッタ法を用いて積分し，80秒間のシ
ミュレーションを行った．
発火したインパルス列( 
に設定)をHanning型のウインドウ
により各時刻での瞬時発火周波数に変換し，これを全てのユニットに
ついて足しあわせたものを出力とした．
入力信号には周期10秒，振幅0.05，平均値0の閾値下の正弦波を
用いた．
様々な雑音レベルをもつ白色雑音，1/f 雑音，ブラウ
ン運動について各々20回ずつシミュレーションをおこない，合
成出力と入力信号の相関係数を求めた結果を図
5Bに示す．興味深いことに，1/f 雑音をノイ
ズ源として印加すると，白色雑音やブラウン運動よりも
低いノイズレベルで，高い信号検出力を実現することが
示された（図 5B）．もちろん，これはあくまで
コンピュータ上での話であり，生体においてこのような
ことが実際に起こっているのかどうかは実験的に確かめ
なければならないのだが， 生体信号によく見られる
1/f ゆらぎの存在意義を考えるう
えで重要な事実ではないかと考えている．
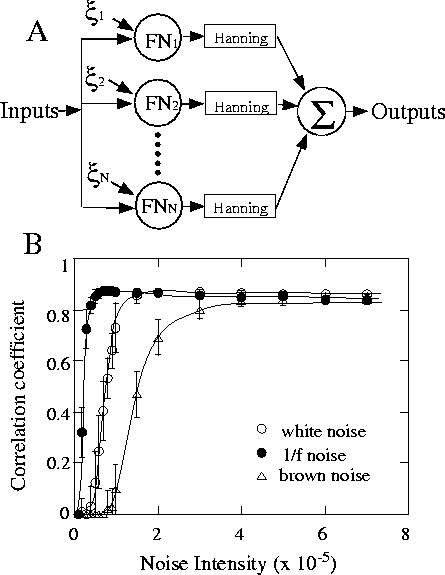
Figure 5: Collinsらが用いた確率共振を示す神経ネット
ワークモデル(A)[37]．
閾値下の正弦波入力に対す
るFHNニューロンネットワークが示す確率共振の結果(B)．
印加される雑音が 1/f 雑音の場合，白色雑音やブラウ
ン雑音に比べ，より低い雑音レベルでの信号検出力に優
れている．
「生理学とカオス」ということで，現在までの研究の流 れを概観した．これまでの時系列解析，モデルによるア プローチは，カオスの存在の証明のみにとらわれていた が，我々としては今後はあくまで生体機能との関連から カオスが語られるべきだと主張したい．ただし，生体シ ステムの解析が決定論一極に偏向することは，必ずしも 合理的なことではない．生体システムの中には決定論，確率 論的システムが共存しているようなものを考えることは 容易である．合原がいうように [38]双方の観点からアプロー チしていくことが重要である．
生理学とカオス
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 jres_7.
The translation was initiated by Yoshiharu Yamamoto on 1998年06月06日 (土) 14時24分27秒 JST
の変化ま
でを説明できるだろうか？
