山本義春
June 6, 1998
手首に指をあてて、時計をみながら脈を計ってみる。最近の時計は、 たいがい秒針が「カチッ、カチッ」と動くか、デジタル表示が1秒毎に 更新されるものが多いので、脈拍すなわち心臓の拍動と「変化−停止」 を規則的にくり返す時計との類似性は明らかである。このような 変化のくり返しをリズムと呼ぶなら、確かに心臓の拍動はリズミック である。
ただし、心臓の拍動によって振子の等時性が発見されたという 逸話の真偽のほどはともかくとして、少なくとも心拍動は等時的ではない。 心電図のR波と呼ばれる特徴的な波形の出現する時間間隔を計測して 1拍毎に表示してやると、図1Aにみられるように一見不規則ともいえる 変動を示すのである。すなわち、心拍リズムは大きく「ゆらいで」いる。 図1Aは、ヒトの安静仰臥位における1拍毎のR-R間隔の 変動(``瞬時''心拍数の逆数であることから心拍変動とも呼ばれる)で あるが[1]、その間隔系列あるいは時系列の標準偏差は、実に100msの オーダーにも及ぶ。コンピュータでR-R間隔を読み取るときの誤差は 高々2〜3msであるので、S/N比は50に達する。生体計測にともなう 誤差としては、非常に小さいといえるだろう。
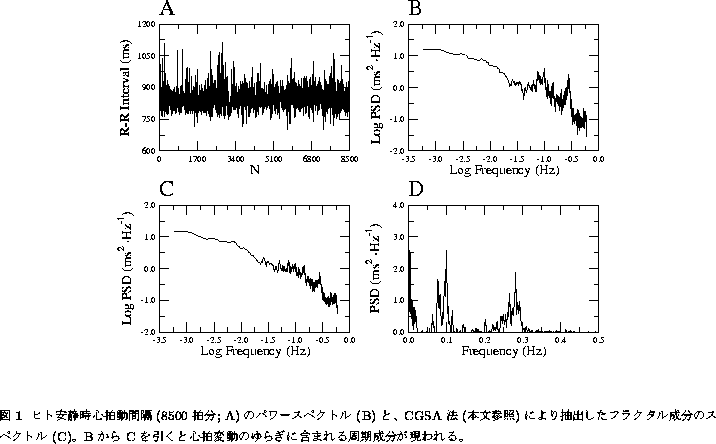
このような心拍変動の成因に関する研究に火をつけたのが、1981年に 発表されたAkselrodらの論文[2]である。彼女らは、イヌの 心拍変動時系列のスペクトル解析を行い、約0.1Hz(周期約10秒) および約0.3Hz(約3秒)の周波数帯域に特徴的なゆらぎ(スペクトルの ピーク)が存在することを発見した(後述するが、図1Dにその例が 示されている)。すなわち一見不規則にみえる 心拍変動も、実は「複合正弦波＋ノイズ」として簡略化できるという モデルを提出したわけである。さらに彼女らは、心臓のペースメーカー 細胞を支配している自律神経を薬理遮断することにより、スペクトルの ピークの大きさが変化することを示した。このことにより、従来は 困難であったヒト自律神経活動の簡便な評価が可能となるかも知れないとの 期待から、その後「心拍変動のスペクトル解析」は主として臨床医学 の分野で広く流行することになる。
一方Akselrodらの論文と同時期に、わが国のKobayashiとMusha[3]が、
ヒトの心拍変動について全く異なった視点からの解析を行っている。
彼らはヒトの安静時心拍変動を長時間測定し、そのスペクトルを両対数軸
に表示してみた。すると特徴的なピークは確かに存在するものの、全体としては
「対数パワーが対数周波数に反比例する」といういわゆる1/f ゆらぎ
のスペクトルをもつことが分かった(図1Bに再現してある)。Akselrodらの
論文では「〜＋ノイズ」とされていた部分(前述のとおりこれは測定誤差
ではない)が、べき型にスケーリングされた周波数構造を有していたという
ことになる。心拍変動をはじめとする生体ゆらぎにおいて、べきの指数
(スペクトル指数 
と呼ばれる)は常に1ではないので、ここでは
このようなべき型のスペクトルをもつゆらぎを 
ゆらぎと総称すること
にする。
さらに時期を同じくして、同様にべき型のスケーリング則をもつ幾何学構造を 扱う「フラクタル幾何学」の流行が起こり、さらにある種のカオス力学系が 相空間でフラクタル構造をとることなどが発見されたことなどもあり、 心拍変動は、生体におけるカオス・フラクタルの研究の主役の一人と なっていった[4]。
以上のような歴史的背景を踏まえ、本論文では、心拍変動をはじめとする 生体ゆらぎのフラクタル性の起源についてのその後の知見について、筆者らの 研究成果を中心に紹介する。また、生体のフラクタルゆらぎがもつ生理学的 あるいは機能的意義についても若干の考察を加えたい。その前にまず 準備として、時系列のフラクタル性とは何か、それをどのように分析するかと いった問題についての解説から始めよう。
ゆらぎとフラクタルとの関係については、実はそれほど単純ではない。
このことを示すために、まず ゆらぎとひと口に
いっても、さまざまなものがあるということを確認しておく。そのために、
逆フーリエ変換によって、 型パワースペクトルをもつ時系列を
つくってみることにする。
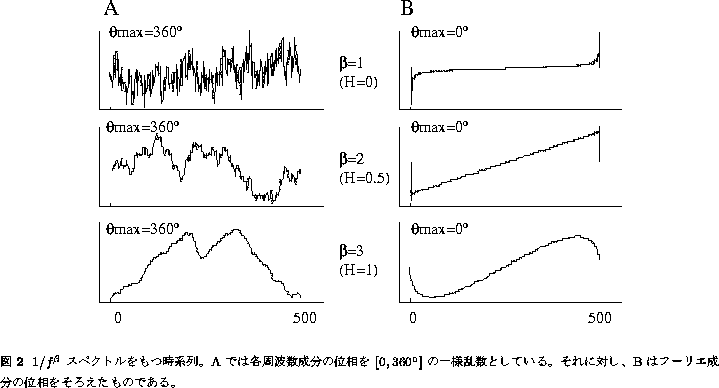
図2にスペクトル指数 が 1, 2, 3 の場合の時系列データを
示す。図2A、Bの両時系列は一見まったく異なってはいるが、実は同じ
をもつ ゆらぎである。同じ をもつにもかかわらず、
時系列がこのようにまったく異なった様相を示す理由は、各周波数成分の
位相の混ざりぐあいの違いにある。図2Aでは各周波数成分の位相を
の一様乱数としている。この場合には、
各時系列は非常に不規則にみえる。ところが各周波数成分の位相を
そろえた場合( 
; 図2B)、時系列の様相は
一変し、この場合、時系列に不規則さはみられない。
このように 性の起源は、非正弦波状の規則的な変化に
よるものと変動の不規則さ自体によるものの二つに分けられる。
前者については、トレンドの混入によるものとの説明がつく場合もあるが、
後者については、その不規則性が何に起因していて、どんな意味をもつのか
は自明ではない。
一見不規則な様相を呈する ゆらぎが
生成される原理を考えるとき、そのパワースペクトルに捕われた考え方を
すれば、べき型にスケーリングされた多数の周波数成分がつくりだされる仕組みが
必要となる。しかし、もっと単純なシステムからも ゆらぎは
生成される。これまでに提案されている ゆらぎの生成原理とし
ては、(少し厳密さを欠くが)相異なる線形フィルターのカスケード
(フィルターの遮断周波数を 
とすれば、Lorentz 型
スペクトルの重ね合せにより 
で 1/f スペクトルが
観察される)[5]、入力の統計雑音が非線形システムにより変調された
場合[6, 7, 8]、セルオートマトン[9]やニューラルネット[10]
などの分散型システムの大域的性質、間欠性カオス[11, 12]、などがある
(まだまだたくさんある)。間欠性カオスのみが完全な自励系であるが、
他はいずれも、ある意味ではノイズが系を駆動する形式を有している。
このような``ノイズ駆動型''の ゆらぎのモデルの代表的なものが、
フラクショナルブラウン運動[13]である。通常(1次元の)ブラウン運動
B(i)は、白色ノイズの加法過程として表現され、その分散は
と書けるが( 
は集合平均)、MandelbrotとVan Ness[13]は
この性質を拡張して、
をフラクショナルブラウン運動と呼んだ。パラメーター0<H<1は
Hurst指数と呼ばれ、変動の不規則さを変化させる役割を果たす(図2A)。
(1)式で 
とおくと、
が導かれる(ただし 
とおいた)。
この(2)式は、時間の尺度をh倍にして構築した
時系列 
の分布型が、大きさが 
倍になる他は、もとの
時系列 
の分布型と同一であるという、自己相似(自己アフィン)
の性質を示す。それゆえこのような性質を持つフラクショナルブラウン運動は
フラクタル的であると呼ばれ、実際Mandelbrotの有名な著書``The Fractal
Geometry of Nature.''[14]でも、このHをさまざまな値に変えること
により自然界に存在する複雑なかたちを表現できるという例が、美しい
コンピュータグラフィクスとともに多数示されている。
フラクショナルブラウン運動の特徴は、スペクトル指数 により抽出できる。
高速フーリエ変換等を用いてゆらぎのパワースペクトルを計算し、その両対数グラフの
傾きより を求めることは、変動が純粋なフラクショナルブラウン運動である
ならば、非常に精度の高い方法とされている[15]。また、このよ
うな純粋なフラクタル時系列に対しては、(2)式の性質を利用した
ユニークな方法も提案されている[16]。しかし、これらの方法を
現実の生体時系列データに応用する場合には注意を要する。
まず第一に、 型パワースペクトルを持つことがフラクタル的であるための
十分条件ではないことは前章でも述べた(図2)。図2A、Bの両時系列を区別できる
ような解析法が欲しいところである。第二に、変動がフラクタルな成分だけでなく
明らかな周期的な成分を含む場合、既存の方法[15, 16]では正確に \
(あるいはH)を求めることが困難となる。実際、心拍変動のパワースペクトルに
周期的な変動成分（スペクトルのピーク）が観察されることは冒頭で述べたとおり
であり、このようなピークは分離して評価されるべきと考えられる。
粗視化スペクトル(Coarse Graining Spectral Analysis; CGSA)法[17]は、
このような明らかな周期成分や位相のそろった広帯域信号と、フラクタル的な(位相の
混った)成分とを分離するための手法である。原理としては、原時系列とそれを粗視化
した時系列とのクロススペクトルの位相を計算すると、前者では時間の経過とともに
規則的に変化するのに対して、後者では不規則に変化するとの性質を利用している。
そして、クロススペクトルの計算値から規則的に変化する成分を排除するアルゴ
リズムが用いられている。もし変動が純粋なフラクショナルブラウン運動で
(2)式を満たすとすると、 と のクロススペクトルの
ゲイン( で規格化したもの)と のパワースペクトルとが等しくなる
ため、与えられた時系列に占めるフラクタル成分の割合( 
)は100 %と
なるだろう。それに対して、ゆらぎに強い周期性がみられたり、図2Bのように
フーリエ成分の位相がそろって滑らかになってしまった場合は、 の
値も低くなることが予想される。
そこで、フラクショナルブラウン運動のフーリエ級数展開
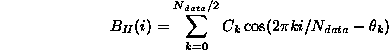
において( 
はデータ数)、位相 
を 
なる一様乱数として与え、さらに 
を の
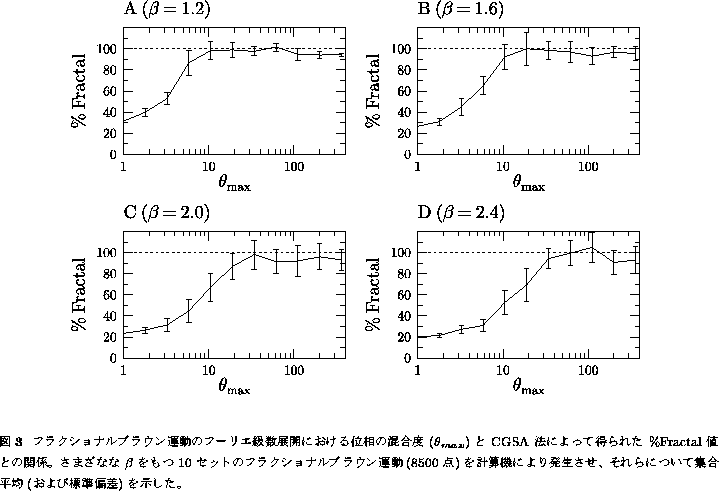
間で変化させることによって の値がどのように
変化するかを調べてみた(図3)。
さまざまな の値をもつフラクショナルブラウン運動について、
とCGSA法によって得られた 値との関係をみると、 が
0に近いうちはゆらぎが図2Bのように滑らかであり、その時は確かに は
低値を示す。しかしながら、 が大きく位相 の混ざり
ぐあいが増えるにつれ、ゆらぎには不規則性が認められるようになり(図2A)、
値も理論通り100 %を示すようになった(図3)。またこの他に、
純粋なフラクショナルブラウン運動に同じ分散を持つ正弦波を加えた場合、
が理論通り50 %になることなども確認されている[17]。
さて、道具立てが整ったところで、実際の心拍変動を分析してみよう。
実は図1は、筆者らがヒトの安静時心拍変動を8500拍分、20例測定し、
それにCGSA法を適用した例である[1]。心拍変動は全体としては 型の
スペクトルをもつが、Akselrodら[2]のいうように、いくつかの周期成分の
混入も示唆される(図1B)。CGSA法によってフラクショナルブラウン運動のみを
抽出すると(図1C)、確かにきれいな 型のスペクトルが得られる。
20例の平均では、このようなフラクタル的変動の全分散に占める割合は実に
85.5 %であった。
少し生理学的にいうと、残りの約15 %の周期成分(図1D)については、その 起源が比較的よく知られている[18]。まず0.1Hz付近に存在する周期成分は、 もともと血圧にそのような波があり、それが動脈血圧反射を介して生み出された ものであると考えられている。ヒトにおいて、脳への灌流血圧を維持するための 反射は極めて重要であるが、血圧が低下すれば心拍数を増やして灌流圧を 上昇されるという反射(フィードバック調節)が働いているので、血圧の波が 心拍変動に反映されるというわけである。一方0.3Hz付近の周期成分は、呼吸と 同期していることが知られている。心拍数は、主として肺の受容器からの反射 入力により(これには異論もあるが)、吸気を行えば上昇し、呼気時に低下するという 性質がある(呼吸性不整脈)。この反射の意義ははっきりと分かっていないものの、 新鮮な空気を吸い込んだ時に頻脈が起こるというのは、ある意味では合目的的 なことかも知れない。
これらの反射の中枢は延髄、遠心路は交感神経系および副交感神経系より成る 自律神経系であり、したがって心拍変動のスペクトル解析を行いそのピークの大きさを 調べることによって自律神経系の活動状況を評価できる、というのが Akselrodらの論文[2]の主張であった。これに対して、CGSA法による 解析結果は、確かにそういうこともあるかも知れないが、それは心拍変動の ほんの一部(約15 %)についていえることで、心拍リズムにみられるゆらぎ のほとんどは、このような``反射性''自律反応以外に起因するかも知れないと 主張する。
筆者らのこれまでの成績では、心拍変動のフラクタル成分は、副交感
神経遮断でその性質が変化する[19]ので、その媒体(mediator)は
自律神経系であること、しかしながら、血圧[20]や呼吸[21]の変動との
同時測定を行った限りは、これらの信号との関連は希薄であること、循環系の
運動負荷[22]や重力負荷[23]によって の値が変化すること
より単なる(無秩序な)ノイズであるとは考えづらいこと、などが明らかに
なっている。
ところで、大勢の人の前にでたり、おそろしい人の前にいるときなど、心臓が ドキドキするのは、誰もが経験的に知っている。これは上記の反射性自律反応 とは別に``情動性''自律反応などと呼ばれ、延髄より上位の視床下部という 中枢(あるいはそこへの情動性入力)が反射性自律反応自体を変調することに よって起こるとされている。最近筆者らは、このような上位中枢からの変調が 心拍変動のフラクタル成分に影響を与えるかどうかを調べる目的で、睡眠の モデルを採用している[24]。
夜間の睡眠中に、脳波(EEG)、眼電図(EOG)、心拍変動(R-R間隔)、血圧などを 連続的に記録し、EEG、EOGなどのデータをもとに睡眠段階を、覚醒期(Awake)、 軽睡眠期(Light; 第1および第2段階)、深睡眠期(Deep; 第3および第4段階)、 REM睡眠期(REM)に分類する(図4)。
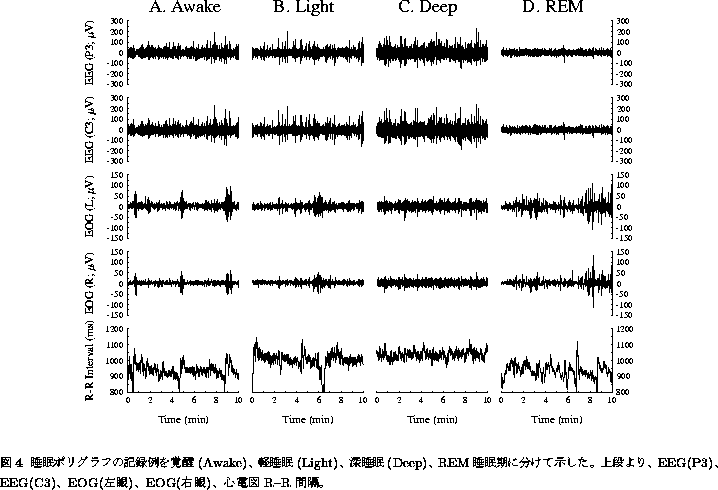
注目すべきは、大脳の深い休息期であるとされる深睡眠期の心拍変動の
時系列には、フラクタル成分特有の``うねり(英語ではwaxing and wanning
などともいう)''がみられず(図4C)、逆に夢見との関連が深いとされる
REM睡眠期の心拍変動(図4D)は、覚醒期の心拍変動パターン(図4A)に酷似して
いることであろう。各睡眠段階が10分以上持続した部分から10分間のR-R間隔
データを切り出し、CGSA法によって解析を行うと(被検者7名; 表1)、確かに
深睡眠期には が有意に低下しており、また の値も覚醒期あるいは
REM睡眠期に比べて有意に低く、いわゆる白色ノイズ( 
)により近い
ゆらぎになっていることが分かる。この深睡眠期における の
低下は、実際には呼吸と同期した周期成分の増大をともない、このときの
心拍変動を細かくみると、先行研究[25]と同様、まことにきれいな正弦波状
振動を示すのである。
以上の心拍変動の起源に関する実験結果を模式的に表すと図5Aのようになる。 すなわち、延髄の心臓血管中枢(Cardiovascular Centers)には、血圧の受容器 (Baroreceptors)や心肺受容器(Cardio-Pulmonary Receptors)より、周期的な 入力があり、それらの信号に応じて反射的に周期的な心拍変動 (Heart Rate Variability)が観察される。しかしながら、この反射(Reflex)は 上位中枢により大きく変調(Modulation)を受けており、その結果として入力に はみられないフラクタル成分がみられるというものである。あくまでも これまでの実験結果を説明する仮説の一つに過ぎないが、今後さらに検討を 加える必要があるものと思われる。
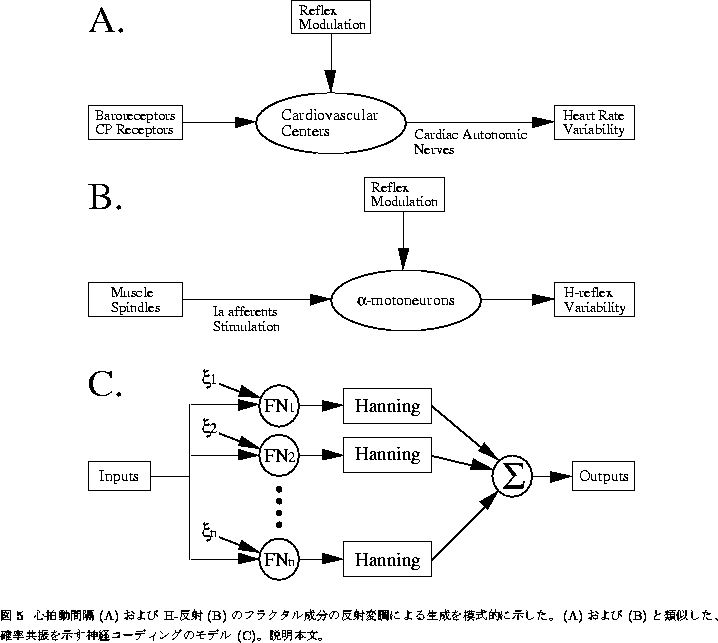
生体のフラクタルゆらぎのモデルとして、確かに図5Aは簡略なものであるが、 恐らく簡略すぎるとの批判は免れまい。というのも、図5Aにおける心臓血管 中枢というのは、実は延髄の数箇所に局在する膨大な神経回路網の集合体 であり、そこでの情報処理の複雑性から考えて、例え入力が周期的であって 反射変調がないとしても出力が(非周期的な)フラクタルゆらぎ、という状況が 十分に考えられるからである。ヒトのからだにおいて、もう少し簡単な仕組みで フラクタルゆらぎのようなものを出す系はないのだろうか?
このような観点から、近年筆者らは、ヒトのヒラメ筋のH-反射にみられる
ゆらぎについて研究を行っている[26, 27]。骨格筋には筋紡錘(Muscle
Spindles)と呼ばれる受容器が存在し、筋長の変化に関する情報をIa求心性神経を
通じて脊髄に送っている。このIa線維は脊髄内でもとの筋を直接支配する
-運動神経(motoneurons)に単シナプス結合し、筋長が伸びればその筋を
収縮させて一定長を保つという一種のフィードバック調節を行っている
(伸張反射; 図5B)。H-反射とは、ヒラメ筋の場合、
膝の裏側を通る脛骨神経を経皮的に電気刺激することによってIa求心性線維の
興奮を引き起こし、結果として誘発されるヒラメ筋の収縮をその筋電図の
大きさによって評価するというものである(図5B)。同じ大きさの刺激に対して
大きなH-反射が出た場合、 -運動神経プールに多くの興奮性入力が入って
おり発火閾値に近い運動神経が多かったというように解釈できる。H-反射が
小さかった場合は、その逆ということになる。
したがって、この場合 -運動神経プールへの興奮性あるいは抑制性
入力の多少というのが図5Bにおける反射変調の役割を果たし、さらには
図5Aの心臓血管中枢の場合と比べて、単シナプス反射という簡単な構造を
有しているとの利点もある。図5Aの自律神経反射と一点だけ異なるのは、
運動神経は平常時においてはほとんど発火しておらず、ゆらぎを調べる際
人為的に(Ia線維に)入力を行ってやる必要があるということである。
そこで筆者らは、まず健常成人において、脛骨神経に1Hzの頻度で1050回、
一定の大きさの刺激を加え、さらに得られたH-反射列を時系列とみなし
(H-reflex Variability; 図5B)、そのゆらぎにCGSA法を適用してみた[26]。
結果として、 が0.9程度、 が90 %以上(この場合は周期入力
が全くないことに注意)と、安静時の心拍変動と類似したフラクタルゆらぎが
観察された。
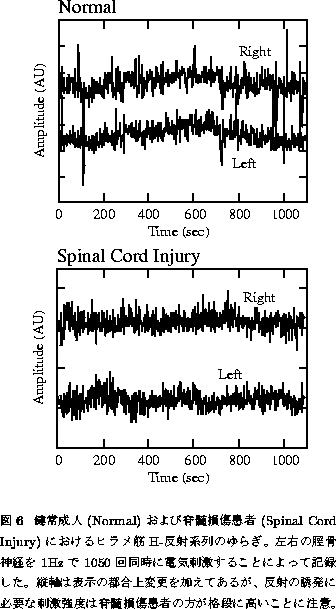
引き続き行われた実験では、今度は左右両脚のヒラメ筋のH-反射を同時に
1050回誘発し、さらに健常成人と脊髄損傷患者との比較を試みた(図6)[27]。
図6上段に示されるとおり、健常成人については左右両脚ともに特徴的なうねりをもつ
フラクタルゆらぎが観察されたのみならず、両脚のゆらぎはかなりの精度で
同期していた。しかしながら、脊髄上位中枢から -運動神経プールへの
(変調)入力の跡絶えた脊髄損傷患者においては、ゆらぎ自体が平坦な白色ノイズ様の
ダイナミクスを示し、かつ両脚のゆらぎは全く無相関であった(図6下段)。
以上の結果より、心拍変動の場合と同様に、運動神経反射は上位中枢により 大きく変調(Modulation)を受けており、その結果としてH-反射のゆらぎに フラクタル性が生まれるという図5Bのような模式図が描ける。この変調が 左右両脚に「同時に」観察されるという事実も、(共通の)中枢性起源を 思わせるといえよう。
実際のところ、ヒトのからだはフラクタルゆらぎ(フラクショナル ブラウン運動)だらけである。心拍変動、H-反射の変動の他にも、 感覚神経における発火間隔のゆらぎ[28]、脳波のアルファ波の ゆらぎ[29]や覚醒を司る中脳ニューロンの発火間隔のゆらぎ[30]、 姿勢動揺[31]や歩行間隔[32]のゆらぎなど、調べられた ものの多くは、例外なくフラクタルゆらぎを呈するといってもよい くらいである。
しかしながら、その割には、このようなフラクタルゆらぎが生体にとって どのような意味をもっているかとの点については、ほとんど分かっていない ようである。フラクタルゆらぎが次々と発見され、「これだけ遍在して いるのだからきっと重要な役割を担っているに違いない」といって興奮していた 頃が随分と懐かしく感じるようになっても、未だに「存在するからには意義が あるのだろう」くらいしかいえないというのも考え物である。そこで本章では、 少し冒険をすることにして、これまでの議論から生体におけるフラクタルゆらぎ の生理学的あるいは機能的意義について何がいえるかについて探ってみる。
その際、まず心拍変動については、現象として循環系の運動負荷[22]や
重力負荷[23]によって の値が変化することが手掛かりとなる
かも知れない。健常成人の安静時心拍変動の は多くの場合1程度なのである
が[1]、これらの負荷時には の上昇が観察され、ブラウン運動と
同程度の 
に近づく。さらには、加齢[33]や心臓病[19]など
でも同様な変化が観察されるようで、図2からも分かるとおり、 が上昇して
(心拍)変動の不規則さが減少するということは、何かよからぬことを示している
ようにみえる。さらにButlerら[23]は、下肢陰圧試験やHead Up Tilt試験に
よって、このレベルまで が増加した場合、かなりの被検者に起立性調節障害
(失神前症状)が観察されたとまで報告している。
これらの現象を無理やり説明しようとするなら、(多少の厳密さ を欠くが)図2を眺めながらフラクショナルブラウン運動の次のような数学的性質を 思い起こすという手もある[19]。
であるので )の
代表的な性質は、過去の
増分と将来の増分との積(ある意味の相関)がゼロとな
ることである。それに対して、安静時心拍変動のよう
にH〜0の場合、この相関は負となることが知られて
いる。すなわち安静時では、過去において心拍数が上昇(低下)すれば
将来それが低下(上昇)する確率が高くなるといった一種の調節作用が
みられる。
(H=1) の場合、
フラクショナルブラウン運動はほとんど原点に復帰しない。
対照的に、安静時心拍変動に対応する 
(H=0) での復帰頻度は、
白色ノイズ( )と同じである( 
ではH=0となる
ことが知られている)。ブラウン運動の場合は、両者の中間に
位置する。何らかの外乱に対して、心拍数をある水準に保つといった
「能力」を考えた場合、安静時( 〜1)はストレ
ス時( 〜2)に比べて、その能力が高いとも考えられる。
安静時心拍変動をフラクショナルブラウン運動とみなした場合の 上記のような統計的性質が、循環系全体の恒常性に果たす役割 については、現時点で明確な結論はない。しかしながら結果としては、 安静時心拍数には、もとの値に復帰するような「力」が働いており、 ストレス時にはこの能力が失われているようにみえるのである。まあ、 この解釈も「存在するから意義がある」という議論の範疇を越えるものでは ない。ただし、生理学的であるかは別として、少なくとも臨床的といえるの かも知れない。
次に、生体におけるフラクタルゆらぎの機能的意義を考える際、図5のような 図式を利用した別の解釈を紹介する。これは近年話題となっている確率共振の 概念[34]を拡張したものである。
確率共振(stochastic resonance; SR)とは、神経細胞などの非線形
システムへの微弱な入力に対する応答性が、一定のノイズの存在下で
増強されるという現象を指し[34]、最近では神経細胞における情報の
コーディングとの関連で注目を浴びている。図5、特に図5Bの運動神経反射の
模式図をみると、いくつかの -運動神経細胞(すなわちプール)に
発火閾値以下の求心性情報が入力され、それが出力へとコーディングされる
かたちになている。前章の実験系では、この細胞を発火させるために
人為的にIa求心性線維に大きな刺激を加えたが、反射変調の信号自体が
ゆらぐ場合、いくつかの神経細胞ではノイズが発火閾値以上に達し、
たとえ平均的には閾値以下の微細な変動に対してでも、出力へとコーディング
される可能性もある。
このような現象を図5Cのようにモデル化し、ノイズの存在が入出力間の
相関を高める、すなわちSRを起こすことを示したのがCollinsらの仕事[35]
である。彼らのモデルは、ある入力S(t)を、神経細胞のダイナミクスの
定性的側面をよく再現するとされるFitzHugh-Nagumo方程式( 
; 添え字i
はi番目のニューロンを表す)
に並列に入力し、発火したインパルス列を幅100ms、面積1sのHanning型の
ウインドウで各時刻での瞬時発火周波数に変換、これを複数(N)個の
ユニットについて足しあわせることによりコーディングされた出力R(t)を
計算するというように、実際の -運動神経プールと極めて類似した
かたちをしている。ただし 
はユニット毎に異なるノイズであり、
。確率共振の程度は、S(t)とR(t)の
相関係数によって評価する。すなわち、相関が高いほど入力情報が出力に
反映されているというわけである。実はこのモデルは、一般に報告されて
いる単一ニューロンの確率共振[34]をアンサンブル平均しただけのもので
あるが、何しろノイズによる反射変調という図5B(図5A?)のモデルとして、
かなりの現実味がある。
ところで、Collinsらの論文[35]では、印加ノイズ として
白色ノイズについてしか調べていない。図5をみる限り、そして前章までの議論に
おいて 型のフラクタルゆらぎ( 〜1)が印加されている可能性が
示されていることを考えると、是非とも様々な をもつフラクショナル
ブラウン運動を白色ノイズの他にも加えてみたくなる。そこで試しにこれを
行ってみた[36]。ただしユニット数はN=100、FitzHugh-Nagumo方程式は
時間間隔0.0001sで4次のルンゲクッタ法を用いて積分し、1秒間のシミュレーション
を行った。入力には周波数10Hzの正弦波を用い、正弦波の振幅Aは閾値下
(A=0.05)あるいは閾値上(A=0.15)に設定した(平均値は0)。
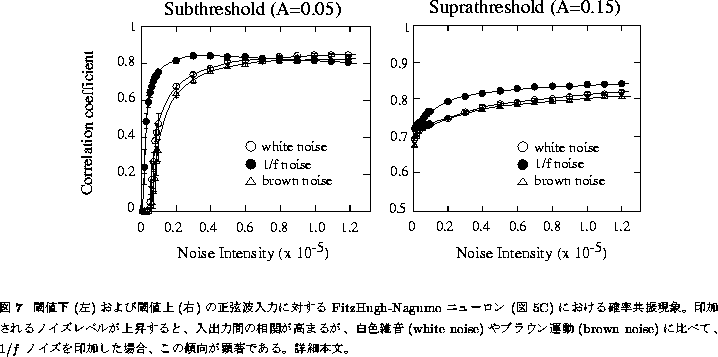
様々な分散をもつ 型のフラクタルゆらぎについて20回ずつシミュレーションを
行い、合成出力R(t)とS(t)(正弦波)との相関を求めた結果が図7に示してある。
正弦波信号が閾値下の場合(図7左)、ノイズがなければニューロンは当然発火しない
わけであるから、入出力の相関はゼロとなる。ノイズのレベルが上昇してこれが
電位 
を発火側に突き上げる頻度が増え、しだいに入出力の相関が出てくる。
図5Cのような複数ユニットの場合、この共振現象はノイズのレベルが上昇しても
単一ユニットの場合と異なりそれほど低下しない[35]。興味深いことに、
入力した正弦波の振幅が閾値下の場合、1/f ノイズ( )は
白色ノイズ( )やブラウン運動( )に比べ、より低いノイズレベル
でも同程度の信号検出力を有していた(図7左)。
一方、正弦波信号が閾値上の場合(図7右)は、ノイズがなくともそもそも発火する ので、入出力の相関はもともと0.7程度と高いレベルにあり、ノイズレベルが 上昇しても、それほど共振の程度が上昇するということはない。ただしこの 場合でも、1/f ノイズの信号検出力は、白色ノイズやブラウン運動に比べて (若干ではあるが)高かった。
実はこの結果は、次のようなフラクショナルブラウン運動の性質を考えれば
直感的に理解できるのである。すわなち、フラクショナルブラウン運動では、
ある時間間隔 
においてトレンドを取り除いたデータの範囲 
すなわち
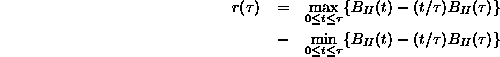
(ただし とおいた)と同じ時間内の標準偏差 
がHurst指数を用いて
のようにスケーリングされることが知られている。これはノイズのレベル
とシミュレーションを行う時間 が同じならば、一般にHが大きい方が
データの範囲(最大−最小)が大きく、ノイズのレベルが低い場合でも電位 を
発火側に突き上げやすくするということを意味する。したがってこの意味においては、
白色ノイズや 1/f ノイズのようなH=0の時系列に比べて、ブラウン運動(H=0.5)の
方が発火を起こしやすいということになる。また、(3)式はトレンドを
除いた上でのはなしであるが、図2にもみられるとおり、一般に ゆらぎの
が大きくなるほど有限長データのトレンド自体も増すので(白色ノイズではゼロで
ある)、1/f ノイズでさえ、白色ノイズよりも発火を起こしやすい。
一方、入力の時間的情報を常に失わずに伝達するためには、ニューロンがいつでも 発火できるような状態になくてはならない。これは、本章冒頭で2.の性質として 示した原点復帰の``頻度''によって表されるが(閾値達したところで原点をリセット することと同じ)、この``頻度''はHの増加とともに小さくなる。
この両者互いに相殺する影響が、シミュレーションを行った時間帯において最適と
となったのが1/f ノイズということなのであろう。したがって、フラクタルゆらぎ
の機能的意義、特に安静時心拍変動やH-反射の変動にみられる 〜1のゆらぎ
の意義として、「最小のノイズレベルで最大の確率共振を引き起こすことが
でき、それが微細な反射入力のコーディングに役立っているかも知れない」という
仮説をたてることも可能である。この仮説は、「なぜ1/f か」という設問にも
一応筋の通った答え与えることができる点で、そのpotentialが高いような気が
する。
正直に告白すれば、平成7年度奨励賞の受賞論文であるから、少しでも立派な ことを書かなければということで、いささか勇み足をしたとの感も拭えない。 特に図5に示したモデルについては、意見を異にする方もさぞかし多いことだろうと 思われる。ただ、生体ゆらぎのフラクタル性の起源やその生理学的あるいは 機能的意義についての研究に参加してきた者の一人として、また、依然として カオス・フラクタルが「見つかった!!」という研究発表に埋もれて閉塞感を 感じている一人として、この場を借りて何か思い切ったことをいってみたい と思ったのであった。若手の一意見として、真摯なご批判をいただければ、 これほど嬉しいことはありません。
(1995年度中山科学振興財団活動報告書「リズムとゆらぎ」, より)
-adrenergic
blockade. American Journal of Physiology 266: R40 (1994)
生体のフラクタルゆらぎとその機能
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 jres_6.
The translation was initiated by Yoshiharu Yamamoto on 1998年06月06日 (土) 14時23分53秒 JST
