山本義春 (東京大学大学院教育学研究科)
February 1, 2000
何らかの測定値が得られたとき、これを
のようにモデル化するという行為は、いわゆる分散分析 などの例を出すまでもなく、今世紀の統計学では常識で ある。さらにつけ加えるなら、このとき誤差は正規分布に従う とされることが多い。その理由は、以下のように説明 される[1]。
いまサイコロを投げて、偶数が出たら真値に 
を足し、奇数が出たら を引くとする。
この試行をn回行い、奇数がr回、偶数がn-r回出た
とすると、真値からのズレは 
であり、
その確率分布は、二項分布の近似として、
平均0、分散 
の正規分布となる。言い換えれば、
``大勢のヒトが一斉に真値からこの操作を始める''と、
蓄積された誤差の分布は正規分布になる、というわけである。
至極当然のような議論ではあるが、この状況をもう一度
図1で確認しておこう。サイコロの連投によって微小誤差
を蓄積していくという過程は、ヒトによって
異なるであろう(あるいは同一の人間が何度も連投をくり返すと
いうことでもよい)。しかしながら、n回目における
ズレの分布を大勢のヒトについて考えた場合、nによらず
正規分布になるということである。真値を知りたい場合は
どうするか。n回目に得られた測定値から``標本平均''を
計算し、それをもって推定値とすればよい。もちろん
推定の精度は、分散 が大きくなると
悪くなる。
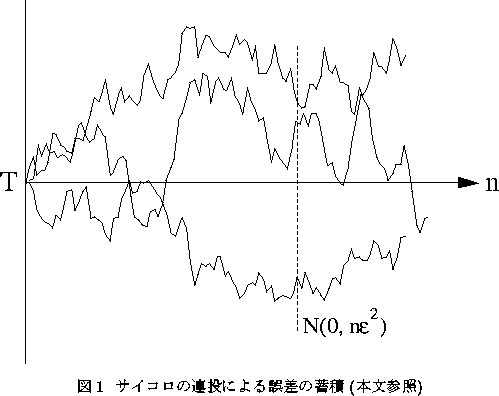
上記の例で、あるヒトがサイコロの連投を1回だけ 行ったときの(ズレの)変化を考える。これは(1次元の) ブラウン運動であり、逸話的に次のように説明される[2]。
水面に浮かべた微粒子(花粉?)が熱運動している水の分子に
衝突される。1回の衝突では動きもすまいが、ときに同じ向きの
衝突が重なる。そうすると微粒子は少しだけ動く。しかし、
動けば水の抵抗を受けるから、すぐに動きは止むだろう。
また、いくつか水の分子の衝突が重なって 
、
(くり返し)微小偏位が観察される。
お分かりのとおり、この微小偏位は上記の例における
であり、温度が高く水の分子の熱運動が
激しい程、あるいは粘性抵抗が小さいほど大きいと考えられる。
事実Tを温度、 
を粘性係数とすると、
が成り立つ。ただしここで、Rは気体定数、 
は
アヴォガドロ数、aは微粒子の半径である。この関係式は、
ブラウン運動の``ゆらぎ(fluctuation)''とエネルギーの
``散逸(dissipation)''すなわち粘性抵抗を結びつけるもので、
揺動散逸定理(fluctuation-dissipation theory)と
呼ばれる[2]。
これは統計物理学の基本定理であって、生体とは直接関係ない
と思われるかも知れない。ここで揺動散逸定理を
持ち出してきた理由は、これが``ゆらぎ(fluctuation)''という
言葉が自然科学用語として用いられている(唯一とは敢えて言わないが)
数少ない例の1つだからである。強調すべきは、通常我々が
誤差と呼んでいるものは、微小なゆらぎ を
(大勢のヒトがサイコロの連投を行うように)``あらゆる場合
において''寄せ集めたものだということである。この意味で、
誤差とゆらぎは本来区別されるべきものかも知れない。
いま、図1のブラウン運動の軌跡をnの関数とみて、 B(n)と書くことにしよう。2つの整数i < jを取ってきて、 B(n)の局所平均、すなわち
を考える。これはnを時刻とみなせば、``時間平均''とでも 呼べるものである。
図1から直感的に分かるとおり、この 
は、
もはや真値Tを与えない。これは、大勢のヒトによる
サイコロの連投の結果を平均すると真値が推定できたのとは
対照的である。このように、例えば(局所的)時間平均が時刻に依存
する変動を、通常``非定常的''であるという[3]。
ブラウン運動のような非定常的な変動では、1本の有限の
軌跡から、真値を求めることが不可能である。
ところで、冒頭で述べたブラウン運動の分散は、
と書けるが(ただしここで、 
は大勢のヒトに
よるサイコロの連投の平均、 
は比例を表し、 
は省いてある)、フラクタルで有名なMandelbrotは、このブラウン運動
の性質を拡張して、
フラクショナルブラウン運動と呼んだ[4]。
H = 1/2の場合がブラウン運動である。彼の著書[5]
では、このHを様々な値に変えることにより、自然界に
存在する複雑なかたちを表現できるという例が、美しい
コンピュータグラフィクスとともに多数示されており、
フラクタルあるいは自己相似という概念の普及に役立った。
ブラウン運動(H = 1/2)の場合と異なり、 
の場合は、``ゆらぎ が積み重なって誤差となる
過程がランダムではない''ことを示している。そして
重要なことは、 
もB(n)と同様に非定常な変動で
あり、1本の有限の軌跡から、真値を求めることが不可能なのである。
そして、生体ゆらぎである。 過去10年間の研究によって、自律神経の支配を受ける 心拍動間隔のゆらぎ[6]、感覚神経における発火間隔の ゆらぎ[7]、脳波のアルファ波のゆらぎ[8]や 覚醒を司る中脳ニューロンの発火間隔のゆらぎ[9]、 運動神経の興奮性のゆらぎ[10]、姿勢動揺[11]や 歩行間隔[12]のゆらぎなど、神経系における 様々なゆらぎが、フラクショナルブラウン運動によって 表現できるということが明らかになってきた。 これらの事実は、神経系の活動は、たとえ生体が一定の状態に 保たれているようにみえても本質的に非定常であり、 1個の有限長の記録から、例えば平均発火率などの``真値''を定義 できないということを示している。というよりも、果たして 真値なるものが果たして存在するのか、という点を考慮する 必要性を示していると考えられる。
サイコロの連投と異なり、生体観測の場合、同一の条件で何度も 記録を得ることは困難である。かといって、時間平均は一定値に 落ち着かず、時刻に依存する。生体、特に神経系の活動にみられる ``フラクタルゆらぎ''は、かくして生体時系列の解析や 生体信号の誤差論に大きな問題を提起するのである。
これまで、ゆらぎは統計的雑音によって駆動されるという
前提で論を進めてきた。ブラウン運動の例でいえば、
水分子の熱雑音が微粒子を( だけ)駆動すること
によってゆらぎが生成されたのであった。これに対して、
ここ15年あまりの、カオスの理論を始めとする非線形力学の
諸理論の発展は、生体ゆらぎの研究に新たな視点を提供しつつ
ある。
カオスとは、比較的単純な非線形微分方程式で表される システムが、一見確率的ともいえるような複雑な変動を示す という現象を指す[13]。いかに非線形といえども、 微分方程式自体は完全に決定論的であり、雑音による駆動は 必要としない。それでも、結果的に現われる変動が 確率的なものと区別がつかないというのであるから、 カオスの発見がいかに近代科学に影響を与えたかは容易に 察することができる。
当然のことながら、複雑な生体のゆらぎが実は決定論的 カオスなのではないかとの予想を立てる研究者が相次いだ。 脳波[14]や心拍動[15]のゆらぎが、このような 予想の道具建てとなったのである。予想を実証するためには、 いわゆる``カオスを判別する方法''(例えば[16])が必要 なのであるが、生体ゆらぎの観測データのように、データ長に 限りがあり、かつ測定自体に起因するノイズが少なくない場合、 これらの方法が満足できる解答を与えることは稀で ある[17]。
むしろ、一見複雑にみえる生体ゆらぎが決定論的なシステムに 起因するのではないか、との予想に対して有効なのは、 モデリングによるアプローチであることが多い。 事実、生体ゆらぎに初めてカオスを見いだしたとされる MackeyとGlassの研究[18]では、白血球の変動の 生理学的(というよりも経験的)モデルとして、
という非線形微分差分方程式が用いられた。この高度に非線形 な方程式の出力が、実際の白血球の変動を表すかについては、 例えば``実測値との比較''などの手法で検討されたわけでは ないが、ある種の病理学的な状態を再現するという基準 によって受け入れられているのである。
同様な例は、最近のTagaの研究[19]にもみることが できる。彼は、二足歩行のモデルを非線形振動子と筋骨格 システム、および地面反力の結合として表現した。この モデルをコンピュータ上で実現し、シミュレーションを 行ってみたところ、``歩く''のはもちろんのこと、 ``つまずく''、``坂道で歩幅を変える''などの柔軟な 動作が可能になったという。さらにある条件下では、 一歩一歩の歩行パラメータにゆらぎがみられた。
このように、単にゆらぎの源泉を統計的雑音に求めるので なく、複雑あるいは非線形システムでモデリングすること によって、``ゆらぐ''構造自体を明らかにしていく 試みも行われているのである。
心拍動の間隔は1拍1拍変動するのだが、通常我々は、 そういうことには目をつむって1分間の拍動数を数え、 心拍数とする。それはそれで良いのだが、なぜ1拍ごとに ゆらぐのか、と問うことによって``心拍数とは何なのか'' という新たな視点が加わる[20]。ことによると、 血液を採って成分分析を行う場合であっても、採血という 行為自体がある種の平均化を伴うものであるから、 意味のある情報を見逃しているかも知れない。生体ゆらぎ の研究は、普段は気にすることの少ない我々のからだの働き に注目する、オタクな営みなのである。
以上、かなり大雑把になってしまったが、生体にみられる ``ゆらぎ''についての研究の現状を紹介した。これ以上 詳しい内容の説明は、気鋭の執筆者が揃った今回の特集では、 不要だろう。
(Jap. J. Sports Sci. 14: 471 より)
謝辞: 執筆に際して貴重なご意見を いただいた、南風原朝和 助教授(東京大学大学院教育学研究科)に 謝意を表します。
統計入門. 岩波書店, 東京, 1973.
数理科学 --
数理物理の展開, サイエンス社, 東京, pp86-93, 1990.
-adrenergic blockade. Am. J. Physiol. 266:
R40-R49, 1994.
生体にみられる``ゆらぎ''
This document was generated using the LaTeX2HTML translator Version 96.1 (Feb 5, 1996) Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 jres_3.
The translation was initiated by Yoshiharu Yamamoto on 2000年02月01日 (火) 21時01分05秒 JST