「ヒトの血圧調節系における
確率共振現象−分析手法の概略−」
担当:東京大学大学院教育学研究科
身体教育学コース研究生 日高 一郎
Last Update: 2000.5.24
はじめに
「確率共振」とは、ある系に加えた入力に対する応答が、ある強度のノイズを加えたときにもっとも高まる、という現象であった。
今回の実験では、一定入力(ティルトテーブルによる周期的振動)を加えながら、ノイズ強度を徐々に増やしている。この系での出力は、心拍数(R-R間隔)の変化である。
したがって、確率共振が存在することを示すためには、ティルトテーブルによって引き起こされたR-R間隔の変動をみればよい。
以下では、この実験と同様の手順で得られた、別の実験でのデータを例として用いる。
1.データ構造
測定、保存されたデータは、このような構造になっている。
Time RR SBP DBP RSP1 NCP1 NCP2 TOTAL
0.02 1121 114.1 58.0 26.88 0.9 0.10 1
0.04 1095 109.3 58.5 27.14 -1.8 -0.89 2
0.06 1159 112.2 56.6 15.18 -2.7 -1.98 3
0.08 1193 112.7 55.1 15.71 -8.2 -5.84 4
0.09 1109 108.3 56.1 31.16 -1.8 -1.78 5
: : : : : : : :
39.93 1208 127.3 61.0 -22.23 -30.2 -21.68 2122
39.95 1181 123.9 59.0 -21.16 60.4 10.20 2123
39.97 1195 120.5 56.6 -10.09 2.7 2.97 2124
39.99 1066 111.7 57.1 4.73 -2.7 -1.49 2125
40.00 1027 111.7 61.0 18.39 23.8 12.67 2126Time: 測定開始からの経過時間(min)
RR: 1拍動ごとのR-R間隔(ms)
SBP: 収縮期血圧
DBP: 拡張期血圧
RSP1: 呼吸曲線
NCP1: レギュレータ圧
NCP2: チャンバー内圧
TOTAL: データ数
2.データを眺める
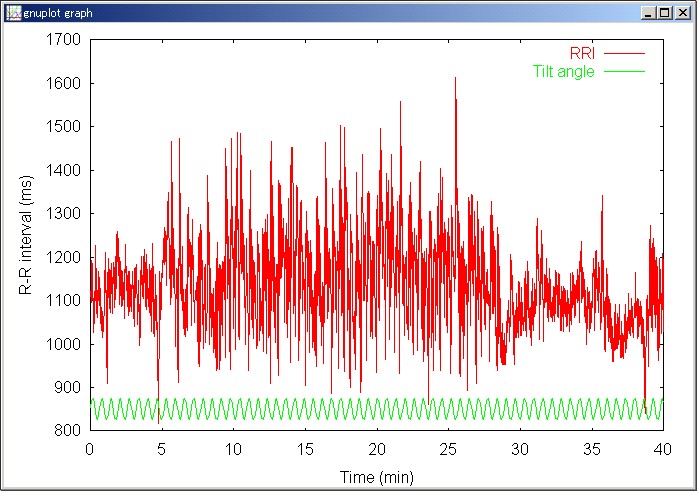
まずは、gnuplotを使って、R-R間隔の時系列を表示してみる。Excelでもよいが、表示できるデータの個数が限られる(65545点)し、遅い。

このように、ノイズが大きくなるにつれて、R-R間隔の変動が大きくなるような雰囲気がある。しかし、R-Rの変動にはティルト角度の変動以外の原因による小刻みな変動が含まれているし、また、もっと長時間での変動(トレンドという)も含まれていることがわかる。そこで、
小刻みな変動 → ローパスフィルタ
トレンド → 局所ロバスト回帰
という方法を使って、もとの信号から不要な変動を除去してやると、みたい現象が見えてくる(かもしれない)。
3.FIRローパス・フィルタ
例えば、ある計測値がこのように変化したとする。
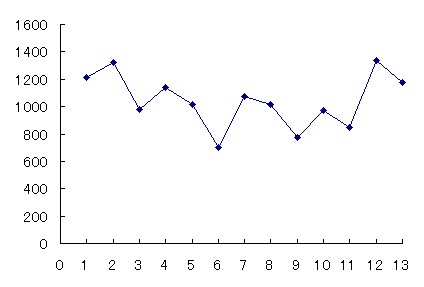
このデータは、下に凸の変化を示しているようだが、小刻みな変動も含まれているため、本来の変化が見えにくい。このような場合、隣接する3つの値の平均値をみるとよい。隣接する3点でやってみると、
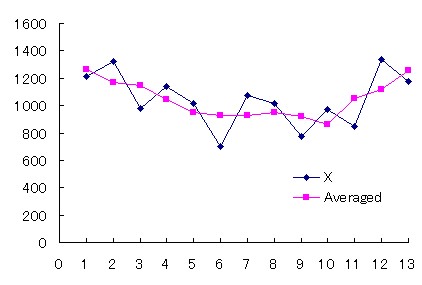
このとき、ある時刻での値は、前の値、現在の値、次の値にそれぞれ1/3をかけたものの和となっている。
この次数(何点のデータを使うか)と係数(それぞれに何をかけるか--それぞれに異なる値を設定してもよい)を変えると、平滑化の度合いが異なってくる。
ある場合には、小刻みな変動だけ除去し、ある場合には大きな変動だけ除去することもできる。
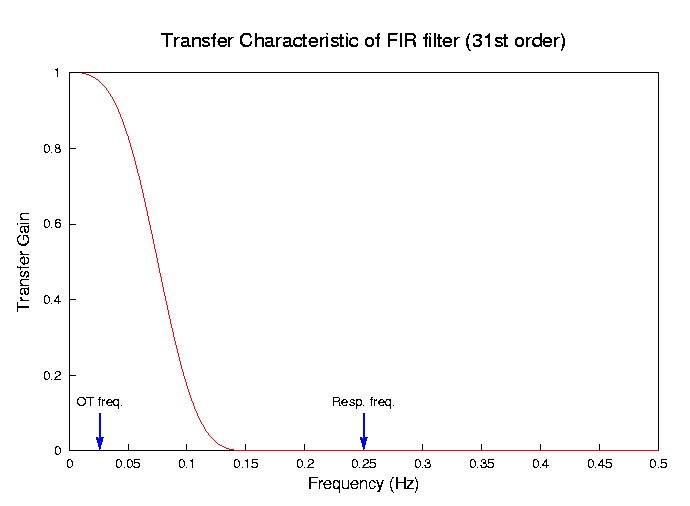
このように、前後の点から現在の値を求めるような操作を「フィルタリング」といい、上記のような係数のセットを、「FIRフィルタ」という。今回は、31次のFIRローパス・フィルタを設計した。
a[1]=0.000711559
a[2]=0.000417876
a[3]=-0.000277043
a[4]=-0.001831765
a[5]=-0.004492046
a[6]=-0.007839536
a[7]=-0.010476442
a[8]=-0.010080779
a[9]=-0.003947292
a[10]=0.010077738
a[11]=0.032568097
a[12]=0.06180586
a[13]=0.093740937
a[14]=0.122757926
a[15]=0.143082138
a[16]=0.150390625
a[17]=0.143082138
a[18]=0.122757926
a[19]=0.093740937
a[20]=0.06180586
a[21]=0.032568097
a[22]=0.010077738
a[23]=-0.003947292
a[24]=-0.010080779
a[25]=-0.010476442
a[26]=-0.007839536
a[27]=-0.004492046
a[28]=-0.001831765
a[29]=-0.000277043
a[30]=0.000417876
a[31]=0.000711559
このようなフィルタにかけたとき、もとのデータの変動のうちどのような変動成分が残るかは、明確に表すことができる。
サンプルデータをFIRローパス・フィルタにかけると、このような時系列が得られる。
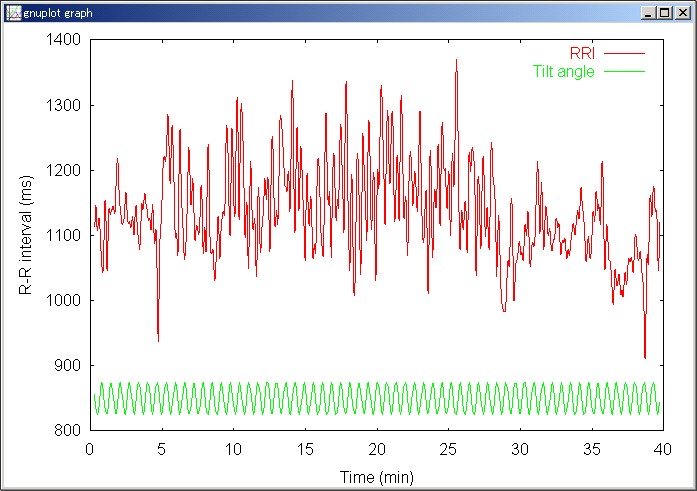
次に、トレンドをとってみる。
4.トレンドの除去
FIRフィルタでトレンドを除去することも可能だが、ゆっくりした成分を取ろうとすると、次数が非常に大きくなってしまう。次数が大きいということは、データの始まりの部分と終わりの部分が使えなくなるということを意味する(例えば、101次のフィルタならば、最初50点、最後50点の挙動は失われる)。
そこで今回は、局所ロバスト回帰という方法を使って、トレンドを求めてみる。
原理は簡単で、データの小区間に注目して、これに直線を当てはめる(どのような直線がもっともよく当てはまるかは、直線とデータとの誤差の2乗の和を基準に決める)。
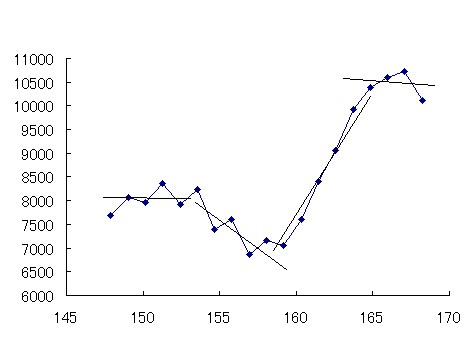
直線に近い点には大きい係数を、遠い点には小さい係数を設定する。
再度直線を当てはめる。ただし、誤差(の2乗)に係数をかけたものの和を基準とする。
すると、最初の直線に近いものは重視し、直線から外れたものは軽視するような直線ができる。このように、はずれ値に左右されない回帰方法を、ロバスト回帰という。
この直線の中央点を、次々に求めていくと、小刻みな変動に左右されないトレンドを求めることができる。
先ほどのローパス・フィルタにかけたデータからトレンドを求め、トレンドを差し引いたものは、こうなる。
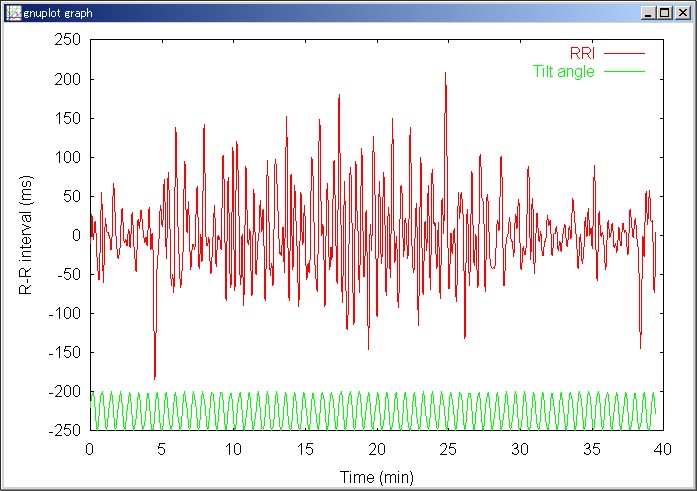
この図だけでも、確率共振の存在を示すのに十分な説得力はあるが、もうすこしスマートな表現方法を考えよう。
5.時間−周波数解析
時々刻々変わるデータの性質を追跡する手法のひとつとして、「時間−周波数解析」というものがある。これは、データの変動を時間的に分解し、また速い変動成分、遅い変動成分を別々に評価できる。
今回は、Wigner-Ville分布を使用した。
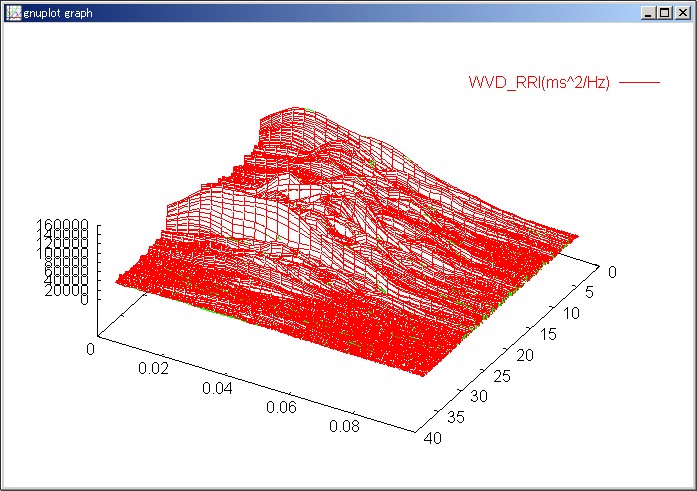
ただし、これでは他の成分の変動も見えてしまうので、わかりにくい。
6.経時変化の表示
Wigner-Ville分布のうち、ティルト角の変化によって引き起こされた成分の変化のみをプロットすると、
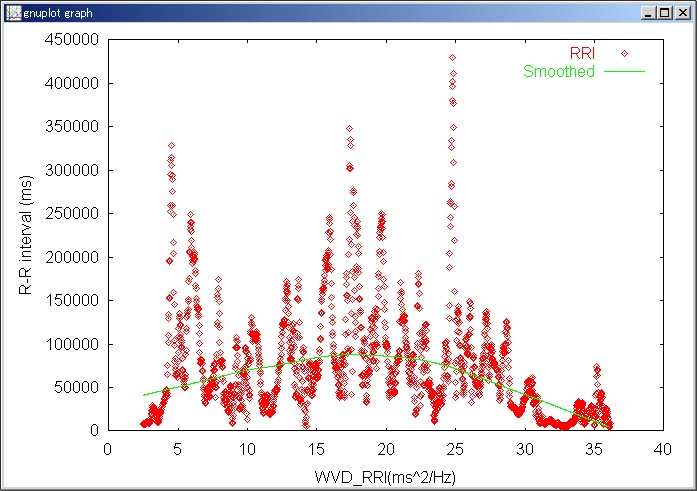
となり、R-R間隔の変動(振幅)自体にも短時間での変動が見られるのだが、大局的に見れば、中間的なノイズ強度でもっとも変動が大きくなるという、確率共振型の変化を呈している。
以上がデータ分析の概略であるが、実際の処理を行う際には、もっと多くのtipsが存在する。